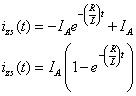Trouver la réponse à l'état zéro d'un circuit parallèle rl
Un circuit parallèle RL premier ordre a une résistance (ou d'un réseau de résistances) et une seule inductance. Circuits de premier ordre peuvent être analysées à l'aide d'équations différentielles du premier ordre. En analysant un circuit de premier ordre, vous pouvez comprendre son calendrier et les retards.
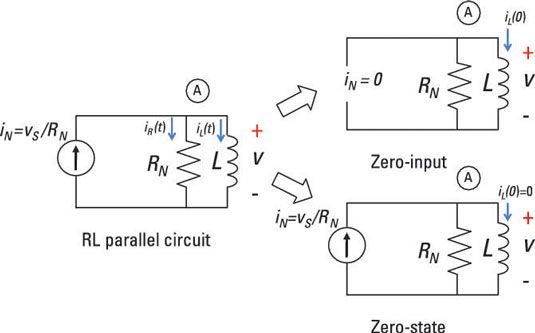
Pour trouver la réponse totale d'un circuit parallèle de RL comme celui présenté ici, vous devez trouver la réponse à entrée nulle et la réponse à l'état zéro, puis ajoutez-les ensemble.
Après jouer avec les maths, vous déterminez que la réponse zéro-entrée du circuit de l'échantillon est la suivante:
Maintenant vous êtes prêt à calculer la réponse à l'état zéro pour le circuit. Signifie réponse zéro-zéro de l'Etat conditions initiales. Pour le circuit-état zéro montré plus tôt, conditions initiales nulles moyens regardant le circuit avec zéro courant de l'inductance au t lt; 0. Vous devez trouver les solutions homogènes et particulières pour obtenir la réponse à l'état zéro.
Ensuite, vous avez zéro conditions initiales et un courant d'entrée de jeN(t) = u (t), où u (t) est une entrée en échelon unitaire.
Lorsque l'entrée de l'étape u (t) = 0, la solution de l'équation différentielle est la solution jeh(t):
Le courant dans l'inductance jeh(t) est la solution de l'équation différentielle du premier ordre homogène:
Cette solution est la solution générale pour l'entrée zéro. Vous trouverez la constante c1 après avoir trouvé la solution particulière et l'application de la condition initiale de l'absence de courant d'inducteur.
Après le temps t = 0, une entrée de l'étape de l'unité décrit le courant dans l'inductance transitoire. Le courant d'inducteur pour cette entrée pas à pas est appelé le réponse à un échelon.
Vous trouverez la solution particulière jep(t) en mettant l'entrée de l'étape u (t) égal à 1. Pour une entrée en échelon unitaire jeN(t) = u (t), remplaçant u (t) = 1 dans l'équation différentielle:
La solution particulière jep(t) est la solution de l'équation différentielle lorsque l'entrée est une étape d'unité u (t) = 1 après t Parce = 0 u (t) = 1 (une constante) après le temps t = 0, assumer une solution particulière jep(t) est une constante jeUN.
Parce que la dérivée d'une constante est 0, ce qui suit est vrai:
Suppléant jep(t) = jeUN dans l'équation différentielle du premier ordre:
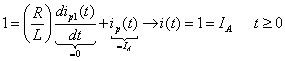
La solution particulière éventuellement suit la forme de l'entrée parce que l'entrée zéro (ou réponse libre) diminue à 0 dans le temps. On peut généraliser le résultat lorsque l'étape d'entrée a une résistance jeUN ou jeUNu (t).
Vous devez ajouter la solution homogène jeh(t) et la solution particulière jep(t) pour obtenir la réponse à l'état zéro:
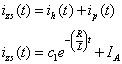
À t = 0, la condition initiale est 0, car ce calcul est à l'état zéro. Pour trouver c1, appliquer jeZS(0) = 0:
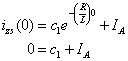
Résolution pour c1 te donne
C1 = -IUN
En substituant c1 dans la réponse à l'état zéro jeZS(t), vous vous retrouvez avec
-
Comment dire une équation différentielle d'un autre -
Analyser un circuit de premier ordre RL en utilisant des méthodes de Laplace -
Équations différentielles pour les nuls -
Trouver les racines d'une équation pondérée -
Définition d'équations différentielles homogènes et non homogènes -
Analyser un circuit de premier ordre rc en utilisant des méthodes de Laplace
Analyser un circuit RC série en utilisant une équation différentielle Un circuit série RC du premier ordre possède une résistance (ou réseau de résistances) et un condensateur connectés en série. Premier ordre circuits RC peuvent être analysées à l'aide d'équations différentielles du premier ordre. En…
Analyser un circuit RLC en utilisant des méthodes de Laplace Utilisation de la transformée de Laplace dans le cadre de votre analyse de circuit vous fournit une prédiction de la réponse du circuit. Analyser les pôles de la transformée de Laplace pour avoir une idée générale du comportement de sortie.…
Décrire circuits de second ordre avec des équations différentielles du second ordre Si vous pouvez utiliser une équation différentielle du second ordre pour décrire le circuit que vous cherchez à, alors vous avez affaire à un circuit de deuxième ordre. Circuits comprenant un inducteur, un condensateur, et résistance…
Composants électroniques: retour dans les amplificateurs de boucle fermée Si vous êtes intéressés à comprendre comment le circuit de rétroaction fonctionne, rappelez-vous cette règle des amplis op électroniques: Si la tension d'entrée est autre chose que zéro, l'ampli op sera saturé, et la tension de sortie sera…
Composants électroniques: comment utiliser un ampli op comme un amplificateur de gain unité UN amplificateur de gain unitaire est un circuit amplificateur électronique qui n'a pas amplifier. En d'autres termes, il a un gain de 1. La tension de sortie dans un amplificateur de gain unitaire est la même que la tension d'entrée.Vous pensez…
Jauge transfert maximum de puissance en utilisant th & # 233-venin de et les théorèmes de norton Th # de théorèmes de Norton 233-venin et peuvent être utilisés pour analyser des circuits complexes en se concentrant sur les circuits de source et de charge. Une application de Th # 233-venin de et les théorèmes de Norton est de calculer la…
Comment détecter une impulsion manquante par un circuit de temporisation Lorsque le chronométrage est éteint votre ordinateur, des événements spécifiques ne se produisent pas dans le bon ordre. Mais si vous savez la physique et je-v relations de résistances et les condensateurs, vous pouvez créer un circuit qui…
Comment résoudre des équations différentielles en utilisant des amplis op Le circuit ampli op peut résoudre des équations mathématiques rapides, y compris des problèmes de calcul telles que les équations différentielles. Pour résoudre une équation différentielle en trouvant v (t), Par exemple, vous pouvez…
Analyser un circuit de RL parallèle en utilisant une équation différentielle Un circuit parallèle RL premier ordre a une résistance (ou d'un réseau de résistances) et une seule inductance. Circuits de premier ordre peuvent être analysées à l'aide d'équations différentielles du premier ordre. En analysant un circuit…
Analyser un circuit parallèle de second ordre RLC utilisant la dualité De second ordre circuits RLC ont une résistance, inductance et condensateur connecté en série ou en parallèle. Pour analyser un circuit parallèle de second ordre, vous suivez le même processus d'analyse d'un circuit série RLC.Voici un exemple…
Trouver la réponse totale d'un circuit parallèle rl Après avoir trouvé la réponse à entrée nulle et la réponse à l'état zéro d'un circuit RL parallèle, vous pouvez facilement trouver la réponse totale du circuit. Rappelez-vous que un circuit parallèle RL premier ordre a une résistance…
Trouver la réponse totale d'un circuit RC série Après avoir trouvé la réponse à entrée nulle et la réponse à l'état zéro d'un circuit RC série, vous pouvez facilement trouver la réponse totale du circuit. Rappelez-vous que un circuit série RC du premier ordre possède une résistance…
Trouvez les réponses à zéro entrée et-état zéro d'un circuit RC série Pour trouver la réponse totale d'un circuit RC série, vous devez trouver la réponse à entrée nulle et la réponse à l'état zéro, puis ajoutez-les ensemble. Un circuit série RC du premier ordre possède une résistance (ou réseau de…
Comment l'analyse de circuit fonctionne dans le domaine s Des techniques d'analyse de circuit dans le s-domaine sont puissants parce que vous pouvez traiter un circuit qui a signaux de tension et de courant changent avec le temps comme si elle était une résistance-seul circuit. Cela signifie que vous…