Analyse S-domaine: compréhension des pôles et des zéros de f (s)

Transformées de Laplace peuvent être utilisés pour prédire le comportement d'un circuit. La transformée de Laplace prend une fonction dans le domaine temporel f (t), et le transforme en la fonction F (s) dans le s-domaine. Vous pouvez afficher les transformées de Laplace F (s) sous forme de rapports de polynômes dans le s-domaine. Si vous trouvez les racines réelles et complexes (pôles) de ces polynômes, vous pouvez obtenir une idée générale de ce que la forme d'onde f (t) va ressembler.

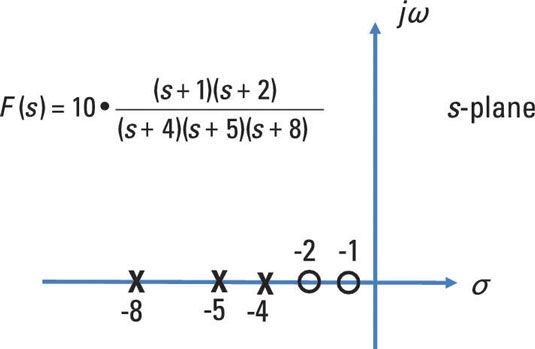
Par exemple, comme le montre ce tableau, si les racines sont réelles, alors la forme d'onde est exponentielle. Si elles sont imaginaires, alors il est une combinaison de sinus et cosinus. Et si elles sont complexes, alors il est une sinusoïde d'amortissement.

Les racines du polynôme dans le numérateur F (s) sont zéros, et les racines du polynôme au dénominateur sont pôles. Les pôles entraînent F (s) soufflant jusqu'à l'infini ou étant undefined - ils sont les asymptotes verticales et les trous dans votre graphique.

Habituellement, vous créez un pôle zéro diagramme en traçant les racines dans le s-avion (réels et imaginaires axes). Le schéma pôle zéro fournit une vue géométrique et l'interprétation générale du comportement du circuit.

Par exemple, considérez la transformée de Laplace suivante F (s):

Cette expression est un rapport de deux polynômes dans s. Affacturage le numérateur et le dénominateur vous donne la description suivante Laplace F (s):

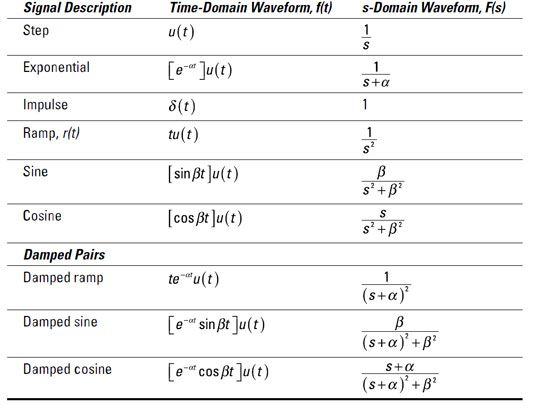
La zéros, ou les racines du numérateur, sont s = -1, -2. La pôles, ou les racines du dénominateur, sont s = -4, -5, -8.

Les deux pôles et les zéros sont collectivement appelés fréquences critiques parce que le comportement fou de sortie se produit lorsque F (s) tend vers zéro ou explose. En combinant les pôles et les zéros, vous avez l'ensemble suivant de fréquences critiques: {-1, -2, -4, -5, -8}.

Ce pôle-zéro schéma trace ces fréquences critiques dans le s-plan, offrant une vue géométrique de comportement du circuit. Dans ce pôle zéro schéma, X désigne pôles et O désigne les zéros.

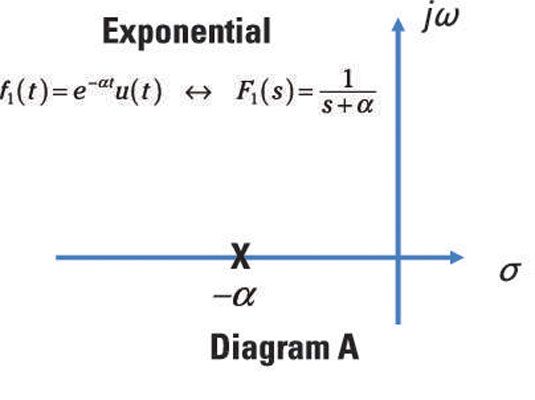
Voici quelques exemples des pôles et zéros des transformées de Laplace, F (s). Par exemple, la transformée de Laplace F₁(s) pour une exponentielle d'amortissement a une paire de transformation comme suit:

La transformation exponentielle F₁(s) a un pôle à s = -alpha et pas de zéros. Ici, vous voyez le pôle de F₁(s) tracée sur l'axe réel négatif dans le demi-plan gauche.

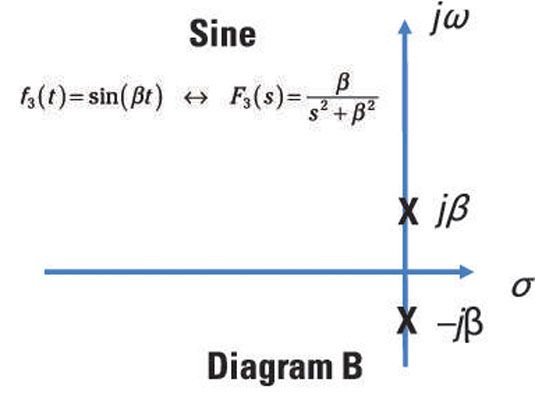
La fonction sinusoïdale a Laplace transformation suivante paire:

L'équation précédente n'a pas de zéros et de deux pôles imaginaires - au s = j +bêta et s = -jbêta. Pôles imaginaires viennent toujours par paires. Ces deux pôles sont non amortie, parce que chaque fois que les pôles sont situés sur l'axe imaginaire joméga-, la fonction f (t) oscillera toujours, avec rien pour amortir it out. Ici, vous voyez une parcelle du diagramme pôle zéro pour une fonction sinus.

Une fonction de rampe a Laplace transformation suivante paire:

La fonction de rampe a des pôles doubles à l'origine (s = 0) et n'a pas de zéros.

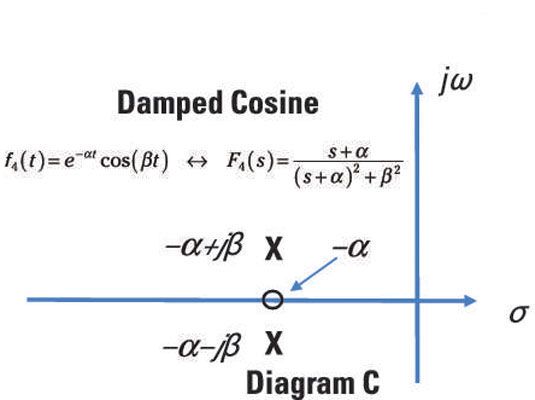
Voilà une transformation paire pour un signal cosinus amorti:

L'équation précédente a deux pôles complexes à s = alpha + jbêta et s = alpha - jbêta et une à zéro s = -alpha.

Pôles complexes, comme pôles imaginaires, viennent toujours par paires. Chaque fois que vous avez une paire de pôles complexes, la fonction a oscillations qui seront amorties à zéro dans le temps - ils ne seront pas durer éternellement. Le comportement sinusoïdal amorti consiste en une combinaison d'une exponentielle (en raison de la partie réelle alpha du nombre complexe) et oscillateur sinusoïdal (en raison de la partie imaginaire bêta du nombre complexe).

Ici, vous voyez représenté le schéma pôle-zéro pour un cosinus amorti.