Systèmes exponentielles

Vous pouvez résoudre des systèmes d'équations algébriques exponentielles lorsque les bases des termes exponentiels sont le même nombre ou lorsque évident

(détestez-vous pas ce mot en mathématiques?) solutions pop parce que des simples natures des équations impliquées. Si les bases match, vous pouvez simplement mettre les exposants égaux les uns aux autres.

Quand une solution algébrique est pas disponible, alors un bon programme de calculatrice graphique ou un ordinateur peut trouver la solution - qui comprend habituellement beaucoup de valeurs décimales et / ou des fonctions logarithmiques.

Cet article traite des types de problèmes que vous pouvez résoudre algébriquement (ou simplement). Bien sûr, le plus simple est juste de brancher un numéro que vous êtes à peu près sûr œuvres. Mais cette méthode peut prendre du temps si vous devez brancher enlève beaucoup - Réserve pour la chose sûre.

Exemples de questions

1. Trouver les solutions communes de

   

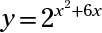
   et y = 16^X+2.

   (2, 65536),

   

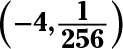
   Vous voulez que les bases pour correspondre, donc d'abord changer le terme exponentiel dans la deuxième équation à une puissance de 2. Il devient y = (2⁴)^{X + 2} = 2^{4X + 8}. Réglage de la deux y-valeurs des deux équations différentes égales les unes aux autres, vous obtenez

   

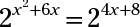
   Maintenant, placez les deux exposants égaux entre eux: X² + 6X = 4X + 8. Déplacement tous les termes à la gauche et de l'affacturage, X² + 2X - 8 = (X + 4) (X - 2) = 0. Les solutions de cette équation quadratique sont X = -4 Ou X = 2. Remplacez le X avec -4 dans l'une des équations originales, et vous obtenez

   

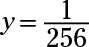
   Remplacer X avec 2 soit dans l'équation, et vous obtenez y = 65536.

2. Trouver les solutions communes de y = 3^{X + 1} et y = 2X + 3

   
   
   
   
   

   (0, 3), (-1, 1). Une calculatrice graphique vous montrera une courbe exponentielle passant de gauche à droite et une ligne apparaissant de couper à travers la courbe en deux endroits près de la y-axe. Vous auriez à agrandir de près pour voir les deux points d'intersection.

   Ces équations ont été choisis avec soin afin que les réponses sont des nombres entiers. Si vous évaluez les deux fonctions pendant quelques valeurs, vous pouvez déterminer les solutions avec un calcul minimal.

   Laisser X = 0 dans la première équation, et vous obtenez y = 3^{0 + 1} = 3. Soit X = 0 dans la deuxième équation, et vous obtenez y = 2 (0) + 3 = 3. Une solution! Laisser X = -1 Dans la première équation, et vous obtenez y = 3^{-1 + 1} = 3⁰ = 1. Soit X = -1 Dans la deuxième équation, et vous obtenez y = 2 (-1) + 3 = -2 + 3 = 1. Ce sont les deux seules solutions.

Questions pratiques

1. Trouver la solution commune (s) de y = 3^{X - 1} et y = 9^X.

2. Trouver la solution commune (s) de y = 8^{2 - X} et

   

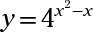
3. Trouver la solution commune (s) de y = 2^X et y = 1 - X.

4. Trouver la solution commune (s) de

   

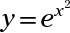
   et y = e.

Voici les réponses aux questions pratiques:

1. La réponse est

   

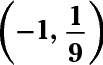
   Régler y égal à y pour obtenir 3^{X - 1} = 9^X. Changez le 9 à 3² et simplifier: 3^{X - 1} = (3²)^X = 3^2X. Maintenant que les bases sont les mêmes, vous pouvez paramétrer les deux exposants égaux entre eux et à résoudre pour x: x - 1 = 2x x = -1. Remplacement de la X avec -1 en y = 3^X-1, vous obtenez

   

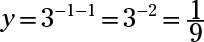
2. La réponse est

   

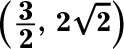
   (-2, 4096).

   Tout d'abord, remplacer l'expression exponentielle dans la première équation pour y dans le second. Puis changer le 8 et 4 pour des puissances de 2, et de simplifier l'équation:

   

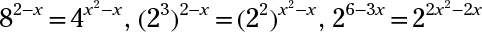
   Les bases sont les mêmes, de sorte que les exposants fixés égaux les uns aux autres: 6-3X = 2X² - 2X devient 0 = 2X² + X - 6. affacturage, vous obtenez 0 = (2X - 3) (X + 2). Quand

   

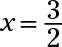
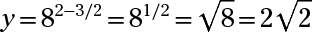
   et quand X = -2, y = 8^{2 - (- 2)} = 8⁴ = 4096.

3. La réponse est (0, 1).

   La première équation est une exponentielle qui augmente de façon constante que la X-valeurs augmentent. Le graphique de la deuxième équation est une ligne qui tombe régulièrement, passant de gauche à droite. Ils se coupent en un point unique. Avec quelques sélections soigneuses de points, vous pouvez déterminer rapidement leur solution commune unique, (0, 1).

   Remplacement de la X avec 0 dans le exponentielle vous donne y = 2⁰ = 1. Et le remplacement de la X avec 0 dans la ligne vous donne y = 1 - 0. = 1.

4. La réponse est (1, e), (-1, e).

   La fonction exponentielle est positif pour toutes les valeurs de X que vous entrez. Et la ligne est horizontale, avec une y-interception de (0, e). Si vous remplacez le X dans le exponentielle avec 1, vous obtenez y = e¹ ou y = e. La même chose se produit lorsque vous remplacez le X -1- avec le carré de -1 est aussi 1, vous obtiendrez la même y-valeur.