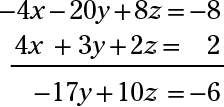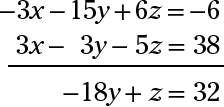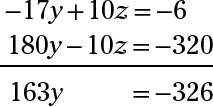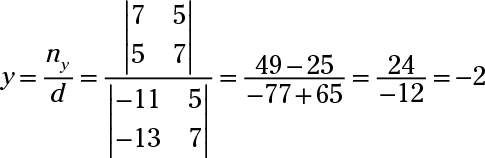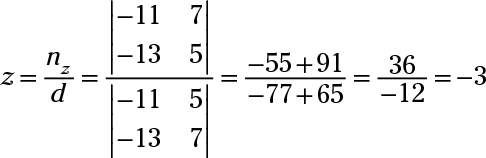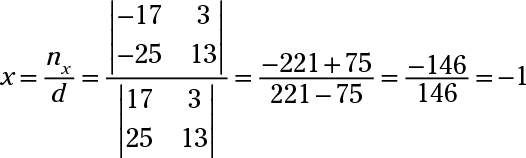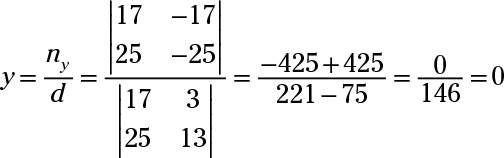Systèmes de trois équations linéaires
Lorsque vous travaillez avec des systèmes d'équations, vous pouvez résoudre pour une variable à la fois. Donc, si une troisième équation linéaire arrive (ce qui porte, bien sûr, sa variable z
), Ainsi, trois est une foule. Cependant, vous pouvez facilement faire face à toutes les variables aussi longtemps que vous vous adressez à tour de rôle.
Vous résolvez les systèmes de trois (ou plus) des équations linéaires en utilisant la méthode d'élimination:
A partir de trois équations, d'éliminer une variable pour créer deux équations à deux variables restantes.
Le premier couplage avec la seconde équation, la seconde avec la troisième, la première ou de la troisième afin d'éliminer l'une des variables. Ensuite, choisissez un appariement différente et d'éliminer la même variable.
De ces deux nouvelles équations, d'éliminer une seconde variable de sorte que vous pouvez résoudre pour celui qui reste.
Substituer de nouveau dans les autres équations pour trouver les valeurs des autres variables.
Branchez la première variable que vous avez résolu pour dans l'une des équations à deux variables que vous avez trouvé à l'étape 1. Puis résoudre pour la troisième variable en branchant les valeurs connues dans l'une des équations originales.
Exemple de question
Trouver la solution commune du système d'équations X + 5y - 2z = 2, 4X + 3y + 2z = 2, 3 etX - 3y - 5z = 38.
X= 4, y = -2, z = -4 - Également écrit que le triplet (4, -2, -4). Vous pouvez choisir de supprimer l'une des trois variables, mais il ya généralement un bon-mieux-mieux-pire-pire décision qui peut être fait.
En ce problème, le meilleur choix est d'éliminer la X variable. La X la seule variable a une coefficient de dans toutes les équations. Vous recherchez un 1 ou -1 ou pour des multiples de la même numéro dans les coefficients d'une seule variable.
Faire deux paires d'élimination. Multiplier la première équation de -4 et l'ajouter à la deuxième équation:
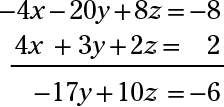
Pour la deuxième appariement, multiplier la première équation de -3 et l'ajouter à la troisième équation:
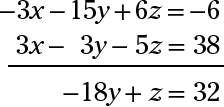
Puis ajouter les deux équations qui en résultent (après la multiplication de la deuxième équation par -10 sorte que vous pouvez éliminer le z's):
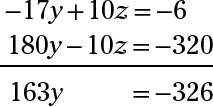
Diviser chaque côté de l'équation par 163 pour obtenir y = -2. Remplace le y à -18y + z = 32 avec le -2, et vous obtenez -18 (-2) + z = 32 + 36 z = 32 z = -4.
Maintenant, prenez les valeurs de y et z et les mettre dans l'une des équations à résoudre pour originaux X. Vous obtenez X + 5 (-2) - 2 (-4) = 2- X - 10 + 8 = 2- X - 2 = 2- X = 4.
Questions pratiques
Trouver la solution commune du système d'équations 3X + 4y - z = 7, 2X - 3y + 3z = 5, et X + 5y - 2z = 0.
Trouver la solution commune du système d'équations 8X + 3y - 2z = -2, X - 3y + 4z = -13, 6 etX + 4y - z = -3.
Voici les réponses aux questions pratiques:
La réponse est X = 4, y = -2, z = -3.
Éliminer X's en multipliant par la troisième équation -3 et en l'ajoutant à la première equation- vous obtenez -11y + 5z = 7. Puis éliminer Xest dans une autre combinaison par multiplication de la troisième équation originale de -2 et de l'ajouter à la deuxième equation- vous obtenez -13y + 7z La règle de Cramer = 5. Utilisez sur ces deux équations résultantes:
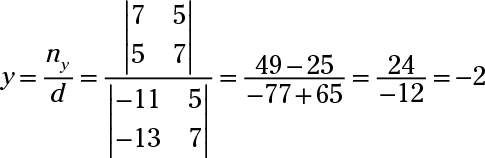
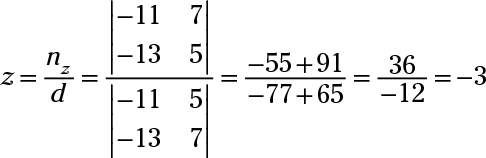
Maintenant, pour substituer -2 y et -3 pour z dans la troisième équation originale pour résoudre X. Vous obtenez X + 5 (-2) - 2 (-3) = 0- X - 10 + 6 = 0- X - 4 = 0- X = 4.
La réponse est X = -1, y = 0, z = -3.
Éliminer z's par multiplication de la première équation par deux et en l'ajoutant à la seconde équation pour obtenir 17X + 3y = -17. Puis éliminer zest dans une autre combinaison en multipliant par la troisième équation 4 et l'ajouter à la deuxième equation- vous obtenez 25X + 13y = -25. Utilisez la règle de Cramer sur ces deux équations résultantes:
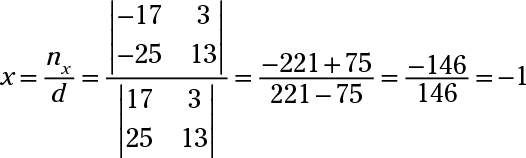
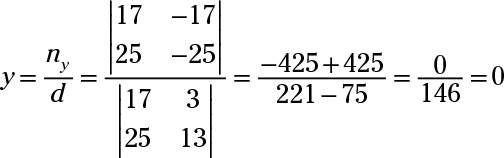
Maintenant substituer X = -1 Et y = 0 dans le troisième équation d'origine pour obtenir 6 (-1) + 4 (0) - z -3- = -6 - z = -3- -z = 3- z = -3.
A propos Auteur
 Résoudre algébriquement deux équations linéaires
Résoudre algébriquement deux équations linéaires Une solution d'un système de deux équations linéaires comprend les valeurs de X et y qui font à la fois des équations vrais - dans le même temps. Graphiquement, la solution est le point où les deux lignes se croisent. Les deux méthodes les…
 Systèmes d'équations linéaires en algèbre ii
Systèmes d'équations linéaires en algèbre ii En algèbre II, équation linéaire se compose de modalités variables dont les exposants sont toujours le numéro 1. Lorsque vous avez deux variables, l'équation peut être représentée par une ligne. Avec trois termes, vous pouvez dessiner un…
 Les bases de la résolution des équations algébriques i
Les bases de la résolution des équations algébriques i L'un des objectifs les plus courants dans l'algèbre I est de résoudre une équation. Résoudre une équation signifie pour identifier le ou les numéros que vous pouvez remplacer la variable avec de faire un énoncé vrai. Vous trouverez…
 Systèmes d'équations en algèbre résoudre
Systèmes d'équations en algèbre résoudre Dans la plupart des cas, une équation algébrique est résoluble que si une valeur est inconnue - qui est, lorsque l'équation a une seule variable. Dans de rares cas, vous pouvez résoudre une équation à deux variables ou plus, car une variable…
 Comment faire pour résoudre les systèmes linéaires qui ont plus de deux équations
Comment faire pour résoudre les systèmes linéaires qui ont plus de deux équations Lorsque votre pré-calcul instructeur vous demande de résoudre plus grands systèmes d'équations linéaires, ces équations impliqueront plus de deux équations qui vont de pair avec plus de deux variables. Vous pouvez écrire ces grands systèmes…
 Comment faire pour résoudre les systèmes linéaires
Comment faire pour résoudre les systèmes linéaires Lorsque vous résolvez les systèmes à deux variables et donc deux équations, les équations peuvent être linéaire ou non linéaire. Les systèmes linéaires sont généralement exprimés sous la forme Ax + By = C, où A, B, et C sont des…
 Comment résoudre des systèmes linéaires en utilisant la substitution ou l'élimination
Comment résoudre des systèmes linéaires en utilisant la substitution ou l'élimination Lors de la résolution de systèmes linéaires, vous disposez de deux méthodes - substitution ou l'élimination - à votre disposition, et celle que vous choisissez dépend du problème. Si le coefficient d'une variable est de 1, ce qui signifie…
 Comment résoudre des systèmes non linéaires
Comment résoudre des systèmes non linéaires Dans un système non linéaire, au moins une équation a un graphique qui ne soit pas une ligne droite - qui est, au moins l'une des équations doit être non linéaire. Votre pré-calcul instructeur vous dire que vous pouvez toujours écrire une…
 Comment faire pour résoudre les systèmes qui ont plus de deux équations
Comment faire pour résoudre les systèmes qui ont plus de deux équations Grandes systèmes d'équations linéaires impliquent plus de deux équations qui vont de pair avec plus de deux variables. Ces systèmes plus importants peuvent être écrites sous la forme Ax + By + Cz +. . . = K où tous les coefficients (K) et…
 Systèmes d'équations utilisées en pré-calcul
Systèmes d'équations utilisées en pré-calcul UN système d'équations est un ensemble de deux ou plusieurs équations à deux ou plusieurs variables. Si le nombre d'équations est égal au nombre de variables différentes, alors vous pourriez être en mesure de trouver une solution unique qui…
 Praxis noyau prep: systèmes d'équations
Praxis noyau prep: systèmes d'équations Le test d'algèbre Praxis Core attendre que vous soyez familier avec les systèmes d'équations. Les équations à deux variables peuvent être résolus si elles sont accompagnées d'une seconde équation d'au moins une des variables.Lorsqu'ils sont…
 Résoudre les problèmes de mots de loi en utilisant un système d'équations
Résoudre les problèmes de mots de loi en utilisant un système d'équations Résoudre les problèmes de mots est l'une des raisons les plus courantes d'utiliser un système d'équations. Par exemple, certains problèmes de mot dans le test ACT Math qu'il serait difficile d'approcher en utilisant une seule variable sont…
 Des stratégies pour résoudre des systèmes d'équations sur l'acte
Des stratégies pour résoudre des systèmes d'équations sur l'acte UN système d'équations est un ensemble de deux ou plusieurs équations qui comprennent deux ou plusieurs variables. Pour résoudre un système d'équations sur le test ACT Math, vous avez besoin d'une équation pour chaque variable dans le…
 Stratégies pour résoudre les équations de loi avec des variables supplémentaires
Stratégies pour résoudre les équations de loi avec des variables supplémentaires Quelques équations sur le test ACT Math peuvent inclure une ou plusieurs des variables supplémentaires. De façon générale, quand une équation a plus d'une variable, vous ne pouvez pas résoudre. En conséquence, dans la plupart des cas, il…