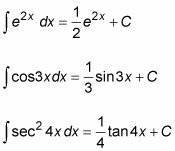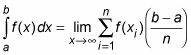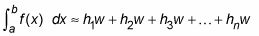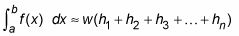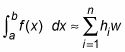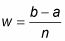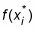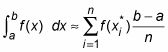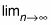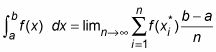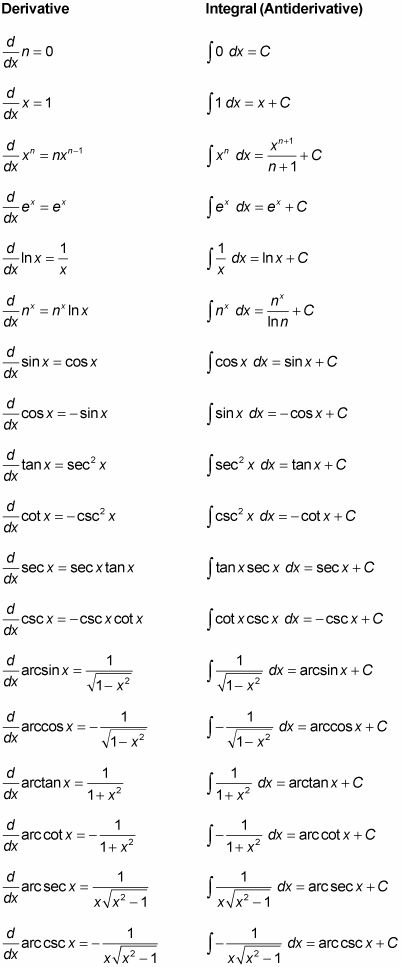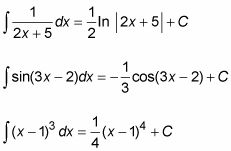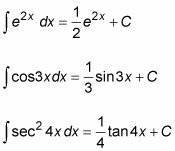Le tableau ci-dessous vous montre comment différencier et intégrer 18 des fonctions les plus courantes. Comme vous pouvez le voir, l'intégration inverse différenciation, de retour de la fonction de son état d'origine, à une constante C
.
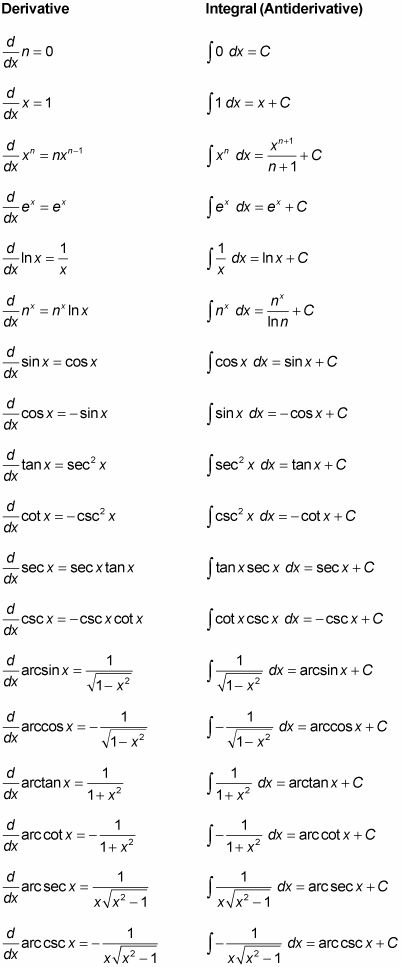
La formule de Riemann Somme de l'intégrale définie
La formule de Riemann Somme donne une définition précise de l'intégrale définie comme la limite d'une série infinie. La formule de Riemann Somme est la suivante:
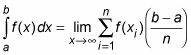
Voici les étapes à suivre pour rapprocher une intégrale en utilisant six rectangles:
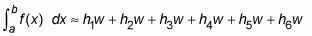
Augmenter le nombre de rectangles (n) Pour créer une meilleure approximation:
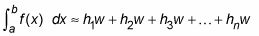
Simplifier cette formule par l'affacturage sur w de chaque terme:
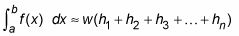
Utilisez le symbole de sommation pour faire de cette formule encore plus compact:
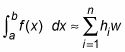
La valeur w est le largeur de chaque rectangle:
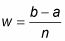
Chaque h valeur est le hauteur d'un rectangle différent:
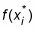
Voici donc la formule de Riemann pour Sum approximation une intégrale en utilisant n rectangles:
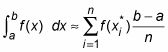
Pour une meilleure approximation, utiliser la limite
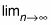
pour permettre le nombre de rectangles se rapprocher infini:
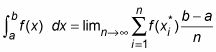
Intégration par parties avec la méthode de DI-agonique
La méthode de DI-agonique est fondamentalement intégration par parties avec un graphique qui vous permet d'organiser l'information. Cette méthode est particulièrement utile lorsque vous devez intégrer par des pièces plus d'une fois pour résoudre un problème. Utilisez le tableau suivant pour l'intégration par parties selon la méthode de DI-agonique:
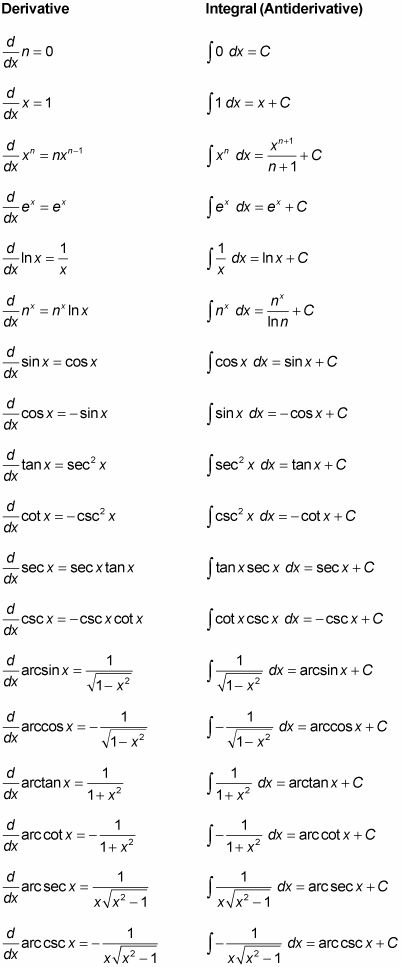
La règle Somme, la Règle multiple constant, et la règle d'alimentation pour l'intégration
Lorsque vous effectuez l'intégration, il ya trois règles importantes que vous devez savoir: La règle Somme, la règle multiple constant, et de l'état d'alimentation.
La règle Somme pour l'intégration vous dit qu'il est normal d'intégrer long terme des expressions par terme. Ici, il est formellement:
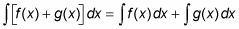
La règle multiple constant pour l'intégration vous dit qu'il est d'accord pour déplacer une constante à l'extérieur d'une intégrale avant de vous intégrer. Ici, il est exprimé en symboles:
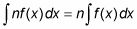
La règle d'alimentation pour l'intégration vous permet d'intégrer un réel pouvoir de X (sauf -1). Voici la règle d'alimentation exprimé formellement:
où n # 8800- -1
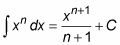
Comment résoudre Intégrales avec Remplacement variable
En calcul, vous pouvez utiliser la substitution de variables pour évaluer une intégrale complexe. La substitution de variable vous permet d'intégrer lorsque la règle Somme, Constant règle multiple, et de la règle d'alimentation ne fonctionnent pas.
Déclarez une variable u, régler égal à une expression algébrique qui apparaît dans l'intégrale, puis remplacer u pour cette expression dans l'intégrale.
Différencier u Pour trouver
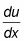
puis isoler tous X variables sur un côté du signe égal.
Faire une autre substitution de changer dx et toutes les autres occurrences de X dans l'intégrale à une expression qui comprend du.
Intégrer l'aide u comme votre nouvelle variable d'intégration.
Exprimez cette réponse en termes de X.
Comment faire pour utiliser l'intégration par parties
Quand vous faites calcul, la formule d'intégration par parties vous donne la possibilité de briser le produit de deux fonctions à ses facteurs et de l'intégrer sous une forme modifiée. Pour utiliser l'intégration par parties en calcul, procédez comme suit:
Décomposer l'ensemble monobloc (y compris dx) En deux facteurs.
Laissez le facteur sans dx égal u et le facteur de dx égal dv.
Différencier u Pour trouver du, et intégrer dv Pour trouver v.
Utiliser la formule:
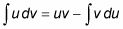
Évaluer le côté droit de cette équation à résoudre l'intégrale.
Comment résoudre fonctions composées où la fonction interne est hache + b
Certains intégrales de fonctions composés F (g(X)) Sont faciles à faire rapidement en calcul. Ceux-ci incluent des fonctions de composés pour lesquels vous savez comment intégrer la fonction externe F, et la fonction interne g(X) Est de la forme hache + b - autrement dit, il se différencie à une constante.
Voici quelques exemples:
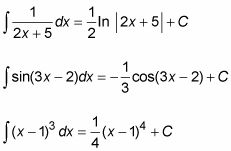
Résolvez fonctions composées où la fonction interne est hache
Lors du calcul des problèmes de calcul, certaines intégrales de fonctions composés F (g(X)) Sont faciles à faire rapidement. Ceux-ci incluent des fonctions de composés pour lesquels vous savez comment intégrer la fonction externe F, et la fonction interne g(X) Est de la forme hache - autrement dit, il se différencie à une constante.
Voici quelques exemples: