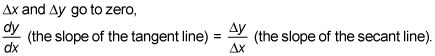Calculer la pente d'une fonction à l'aide du quotient de différence

Vous pouvez calculer la pente d'une fonction en utilisant le quotient de différence. Le quotient de différence vous permet de calculer une pente si vous ne possédez pas d'abord deux points à brancher sur la formule de la pente.

Pour calculer une pente, vous avez besoin de deux points à brancher sur cette formule. Pour une ligne, cela est facile. Vous choisissez deux points quelconques de la ligne et branchez. Mais il est pas si simple, si vous voulez, par exemple, la pente de la parabole F (X) = X² au point (2, 4). Découvrez le premier chiffre.

Vous pouvez voir la ligne tracée tangente à la courbe au (2, 4). Parce que la pente de la tangente est le même que la pente de la parabole au (2, 4), tout ce que vous avez besoin est la pente de la tangente à vous donner la pente de la parabole. Mais vous ne savez pas l'équation de la tangente, de sorte que vous ne pouvez pas obtenir le deuxième point - en plus (2, 4) - que vous avez besoin pour la formule de la pente.

Voici comment les inventeurs du calcul obtenu autour de ce barrage routier. La figure suivante montre à nouveau la ligne de tangente et une sécante coupant la parabole en (2, 4) et au (10, 100).

Définition de sécante: Une sécante est une ligne qui coupe une courbe en deux points. Ceci est un peu simpliste, mais il va faire.

La pente de cette ligne sécante est donnée par la formule de la pente:

Vous pouvez voir que cette ligne sécant est plus raide que la tangente, et donc la pente de la sécante, 12, est supérieure à la pente que vous cherchez.

Maintenant, ajoutez un point de plus à (6, 36) et en tirer une autre sécante utilisant ce point et (2, 4) à nouveau, comme le montre la figure suivante.

Calculer la pente de cette deuxième sécantes:

Vous pouvez voir que ce sécante est une meilleure approximation de la tangente que la première sécantes.

Maintenant, imaginez ce qui se passerait si vous attrapé le point (6, 36) et il a glissé en bas de la parabole vers (2, 4), en faisant glisser la sécante avec elle. Pouvez-vous voir que le point se rapproche et plus proche (2, 4), la ligne sécante se rapproche et plus proche de la tangente, et que la pente de cette sécante devient donc de plus en plus proche de la pente de la tangente?

Ainsi, vous pouvez obtenir la pente de la tangente si vous prenez le limite des pentes de ce mouvement sécantes. Donnons les coordonnées du point mobile (X₂, y₂). Comme ce point (X₂, y₂) Glisse rapproche de (X₁, y₁), À savoir (2, 4), le courir, ce qui équivaut X₁ - X₁, se rapproche et plus proche de zéro. Alors, voici la limite que vous avez besoin:

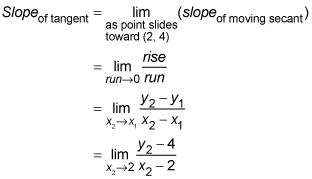
Regardez ce qui arrive à cette limite lorsque vous branchez en quatre points sur la parabole qui sont plus proches et plus proche (2, 4):

Lorsque le point (X₂, y₂) Coulisse à (3, 9), la pente est

ou 5.

Lorsque le point glisse à (2.1, 4.41), la pente est

ou 4.1.

Lorsque le point de glisse (2,01, 4,0401), la pente est de 4,01.

Lorsque le point de glisse (2.001, 4,004001), la pente est 4.001.

Ressembler sûrs la pente se dirige vers 4.

Comme avec tous les problèmes de limites, la variable dans ce problème, X₂ approches mais obtient jamais réellement à la flèche numéro (2 dans ce cas). Si il est arrivé à 2 - qui se passerait si vous glissé le point que vous attrapé le long de la parabole jusqu'à ce qu'il était en fait au-dessus de (2, 4) - vous obtiendrez

qui est indéfini. Mais, bien sûr, la pente à (2, 4) est précisément la pente que vous voulez - la pente de la ligne lorsque le point t la terre au-dessus de (2, 4). Là est la beauté du processus de limite. Avec cette limite, vous obtenez le exact pente de la tangente ligne à (2, 4), même si la fonction de limite,

génère des pentes sécante lignes.

Voici à nouveau l'équation de la pente de la tangente:

Et la pente de la tangente est - vous l'aurez deviné - le dérivé.

Signification de la dérivé: La dérivée d'une fonction F(X) À un certain nombre X = c, écrit

est la pente de la tangente à F tracée à c.

La fraction de la pente

est exprimée avec la terminologie algèbre. Maintenant, vous pouvez réécrire pour lui donner ce look de calcul prétentieux. Mais d'abord, enfin, la définition que vous avez été en attente pour.

Définition de la différence quotient: Il ya un terme de calcul de fantaisie pour la fraction générale de la pente,

lorsque vous écrivez dans la façon de calcul de fantaisie. A est une fraction quotient, droit? Et tous les deux y₂ - y₁ et X₂ - X₁ sont différences, droit? Donc, voil # 224-, on l'appelle le différence quotient. C'est ici:

(Ceci est la façon la plus courante de la rédaction du quotient de différence. Vous pouvez courir à travers les autres, des moyens équivalents.)

Ok, nous allons exposer ce processus dans lequel

se transforme en le quotient de différence.

Tout d'abord, la courir, X₂ - X₁ (dans cet exemple, X₂ - 2), est appelée h. Ensuite, parce que X₁ = 2 et la courir égal à égal h, X₂ est égale à 2 + h. Vous écrivez ensuite y₁ comme F(2) et y₂ comme F(2 + h). Faire toutes les substitutions vous donne la dérivée de X² à X = 2:

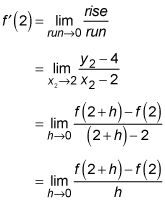
Rappelez-vous que

est tout simplement la contraction

escalier étape, vous pouvez voir dans la précédente figure comme le point glisse vers le bas de la parabole vers (2, 4).

La figure suivante est fondamentalement la même que la précédente, sauf que, au lieu de points comme exactes (6, 36) et (10, 100), le point de glissement présente les coordonnées générales de (2 + h, F (2 + h)), et le augmenter et le courir sont exprimés en termes de h.

Donc, ce chiffre est le graphique ultime pour

Êtes-vous confus par ces deux chiffres? Ne vous inquiétez pas. Ils montrent tous deux la même chose. Ces deux chiffres sont des représentations visuelles de

Faire le calcul vous donne, enfin, la pente de la tangente en (2, 4):

Ainsi, la pente au point (2, 4) est de 4.

Définition principale de la dérivé: Si vous remplacez le point (2, F(2)) dans l'équation de limite avec le point de vue général (X, F (X)), Vous obtenez la définition générale de la dérivée en fonction de X:

Donc enfin vous voyez ce que le dérivé est défini comme la limite du quotient de différence.

La figure suivante montre cette définition générale graphiquement. A noter que cette figure est pratiquement identique à la précédente, sauf que Xs remplacer les 2s dans la figure précédente et que le point mobile dans cette figure glisse vers le bas vers n'importe quel ancien point (X, F (X)) Au lieu de vers le point spécifique (2, F(2)).

Maintenant travailler sur cette limite et obtenir le dérivé de la parabole, F(X) = X²:

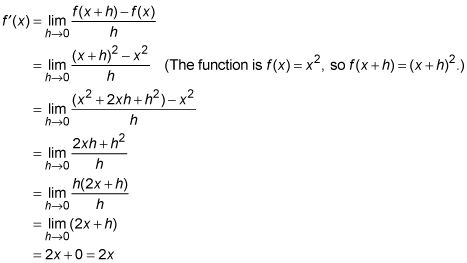
Ainsi, par cette parabole, le dérivé (ce qui est la pente de la tangente à chaque valeur X) Est égal à 2X. Branchez un nombre quelconque dans X, et vous obtenez la pente de la parabole à ce X-valeur. Essayez-le.

Le chiffre tri final des résume (de manière simplifiée) toutes les idées précédentes difficiles sur le quotient de différence.

Comme les trois figures précédentes, le chiffre final contient une pente en escalier de base, une sécante, et une tangente. La pente de la sécante est

La pente de la tangente est

et vous pouvez voir pourquoi il en est l'un des symboles utilisés pour le dérivé. Comme la ligne sécante en escalier réduit à rien, ou, en d'autres termes, dans la limite de