Trouver les zones exactes dans une courbe en utilisant l'intégrale définie

Lorsque l'approximation de la surface sous une courbe en utilisant des rectangles, les rectangles que vous utilisez gauche, à droite, ou milieu, mieux le rapprochement. Donc, "tout" que vous auriez à faire pour obtenir la superficie exacte sous une courbe est d'utiliser un nombre infini de rectangles. Maintenant, vous ne pouvez pas vraiment faire cela, mais avec l'invention fantastique de limites, cette est une sorte de ce qui se passe. Voici la définition de l'intégrale définie qui est utilisé pour calculer les zones exactes.

La intégrale définie ("simple" définition):La zone exacte sous une courbe entre X = un et X = b est donnée par l'intégrale définie, qui est défini comme la limite d'une somme de Riemann:

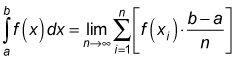
Est-ce une chose de beauté ou quoi? Notez que cette somme (tout à droite de "lim") est identique à la formule de n rectangles de droite, R_n:

La seule différence est que vous prenez la limite de cette formule que le nombre de rectangles tend vers l'infini

Cette définition de l'intégrale définie est la version simple, basé sur la formule de rectangle droite. Vous verrez le vrai McCoy-définition dans un instant, mais parce que toutes les sommes de Riemann pour un problème spécifique ont la même limite - en d'autres termes, il n'a pas d'importance ce type de rectangles vous utilisez - vous pourriez aussi bien utiliser le droit; définition rectangle. Il est le moins compliqué et il sera toujours suffit.

Voici la zone exacte sous F (X) = X² + 1 entre X = 0 et X = 3:

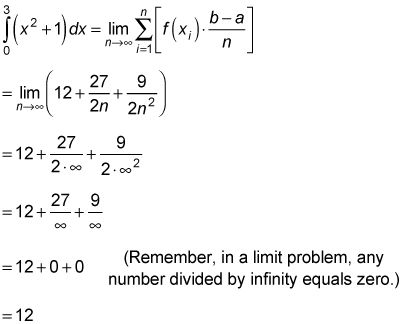
Grosse surprise.

Ce résultat est assez étonnant si vous pensez à ce sujet. En utilisant le processus de limite, vous obtenez une exact réponse de 12 - un peu comme 12,00000000 ... à un nombre infini de décimales - pour l'aire sous la, la fonction courbe douce F (X) = X² + 1, sur la base des zones de rectangles à sommet plat qui courent le long de la courbe dans un déchiquetée, de la mode en dents de scie.

Trouver la zone exacte de 12 en utilisant la limite d'une somme de Riemann est beaucoup de travail (rappelez-vous, vous devez d'abord déterminer la formule de n rectangles à droite). Cette méthode complexe de l'intégration est comparable à la détermination d'un dérivé de la manière dure en utilisant la définition formelle qui est basé sur le quotient de différence.

Parce que la limite de toutes les sommes de Riemann est le même, les limites à l'infini de n rectangles de gauche et de n rectangles médianes - pour F (X) = X² + 1 entre X = 0 et X = 3 - devrait vous donner le même résultat que la limite à l'infini de n rectangles droite. Voici la limite rectangle gauche:

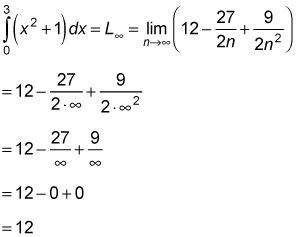
Et voici la limite rectangle milieu:

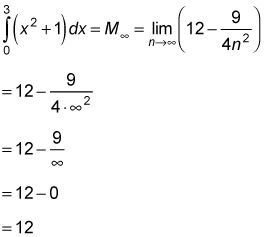
Si vous êtes quelque peu incrédule que ces limites vous le donnent effectivement exact aire sous F (X) = X² + 1 entre 0 et 3, vous n'êtes pas seul. Après tout, dans ces limites, comme dans tous les problèmes de limites, la flèche numéro

est seulement approché- il n'a jamais réellement atteint. Et en plus de cela, ce que cela signifierait pour atteindre l'infini? Vous ne pouvez pas le faire. Et indépendamment du nombre de rectangles que vous avez, vous avez toujours que déchiquetée, bord en dents de scie. Alors, comment peut une telle méthode vous donner la superficie exacte?

Vois-le de cette façon. Jetez un oeil à ces deux figures suivantes.

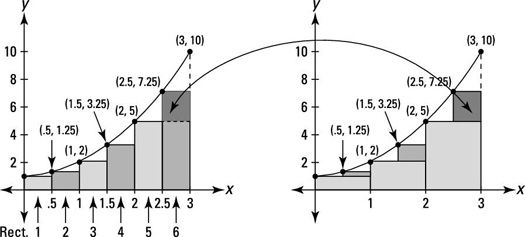F (X) = X² + 1 «. />

Vous pouvez dire à partir de ces chiffres que la somme des aires de rectangles de gauche, quel que soit leur nombre, sera toujours un sousestimer (ce qui est le cas pour les fonctions qui augmentent sur la durée en question).

Et à partir de la figure ci-dessous, vous pouvez voir que la somme des aires de rectangles de droite, peu importe combien vous en avez, sera toujours un plus deestimer (pour les fonctions de plus en plus).

Donc, parce que les limites à l'infini de la sous-estimation et la surestimation sont tous deux égaux à 12, qui doit être la zone exacte. (Un argument similaire fonctionne pour les fonctions décroissante.)

Toutes les sommes de Riemann pour un problème donné ont la même limite. Non seulement sont les limites à l'infini de la gauche, des rectangles à droite, et le point milieu mêmes pour un problème donné, la limite d'une somme de Riemann vous donne également la même réponse. Vous pouvez avoir une série de rectangles avec inégale widths- vous pouvez avoir un mélange de gauche, à droite, et rectangles- milieu ou vous pouvez construire les rectangles afin qu'ils touchent la courbe ailleurs qu'à leur coin supérieur gauche ou à droite ou dans les milieux de leurs côtés supérieurs. La seule chose qui importe est que, à la limite, la largeur de tous les rectangles tend vers zéro (et à partir de Il en résulte que le nombre des rectangles tend vers l'infini). Cela vous amène à l'extrême totalement vers le bas et sale jumbo suivante, Mumbo d'intégration qui prend toutes ces possibilités en compte.

La intégrale définie (réel McCoy définition): L'intégrale définie à partir de

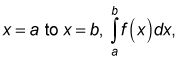
est le nombre de toutes les sommes de Riemann qui ont tendance à la largeur de tous les rectangles tend vers zéro et que le nombre de rectangles tend vers l'infini:

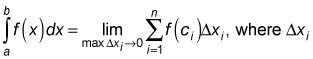
est la largeur de la jee rectangle et c_je est le X-de coordonnées de l'endroit où le jee touches rectangulaires F (X). (Cette

garantit simplement que la largeur de tous les rectangles se rapproche de zéro et que le nombre de rectangles tend vers l'infini).