Comment graphiques de dérivés diffèrent de graphiques de fonctions

Lorsque vous commencez à regarder les graphiques de dérivés, vous pouvez facilement tomber dans la pensée d'entre eux comme des fonctions régulières - mais ils ne sont pas. Heureusement, vous pouvez apprendre beaucoup de choses sur les fonctions et leurs dérivés en regardant leur côté des graphiques à côte et en comparant leurs caractéristiques importantes. Par exemple, prendre la fonction, F (X) = 3X⁵ - 20X³.

Vous allez maintenant déplacer le long F de gauche à droite, une pause de noter ses points d'intérêt et aussi observer ce qui se passe au graphique de

dans les mêmes points. Mais d'abord, consultez la (longue) avertissement suivant.

Ceci est PAS la fonction! Comme vous regardez le graphique de

dans la figure, ou le graphe de tout autre dérivé, vous devrez peut-être vous gifle chaque minute ou deux pour vous rappeler que "Ceci est la dérivé Je regarde, pas la fonction! "Il est facile de confondre graphiques des instruments dérivés à des fonctions régulières. Vous pourriez, par exemple, regarder un intervalle qui se passe sur le graphique d'un dérivé et à tort de conclure que la fonction d'origine doit également être va dans le même intervalle - une erreur compréhensible.

Vous savez la dérivée première est la même chose que la pente. Alors, quand vous voyez le graphique de la dérivée première remontant, vous pouvez penser, "Oh, la dérivée première (la pente) est à la hausse, et quand la pente monte qui est comme monter sur une colline, donc la fonction d'origine doit être en hausse. " Cela semble raisonnable, car, lâchement parler, vous pouvez décrire le côté avant d'une colline comme une pente qui va, augmentant. Mais mathématiquement parler, la face avant d'une colline a une positif pente, pas nécessairement une croissant pente. Alors, où une fonction est croissante, le graphique de son dérivé sera positif, mais ce graphique dérivé pourrait être monter ou descendre.

Dites que vous allez sur une colline. Comme vous vous approchez du sommet de la colline, vous allez encore up, mais, en général, la pente (la pente) va vers le bas. Il pourrait être 3, puis 2, puis 1, puis, au sommet de la colline, la pente est égale à zéro. Donc, la pente devient plus petit ou décroissante, alors même que vous grimpez la colline ou croissant. Dans un tel intervalle, le graphe de la fonction est croissante, mais le graphique de son dérivé est décroissante. Compris?

Bon, revenons à la F et son dérivé dans la figure. Commençant sur la gauche et les voyages vers la droite, F augmente jusqu'à ce que le max locale (-2, 64). Ça va, donc sa pente est positif, mais F est de moins en moins forte si sa pente est décroissante - la pente diminue jusqu'à devenir nulle à la pointe. Ceci correspond à la courbe de

(la pente) qui est positif (parce qu'il est au-dessus du X-axe) mais décroissante comme il descend au point (2, 0). Résumons tout le long de votre voyage F et

avec la liste suivante de règles.

• Un croissant un intervalle de fonction correspond à un intervalle sur le graphique de son dérivé qui est positif (ou zéro pour un seul point si la fonction a un point d'inflexion horizontal). En d'autres termes, l'intervalle de plus en plus d'une fonction correspondant à une partie du graphe dérivé qui est au-dessus de la X-axe (ou qui touche l'axe pour un seul point dans le cas d'un point d'inflexion horizontal). Voir intervalles A et F dans la figure.

• Une locale max sur le graphique d'une fonction (tel que (-2, 64) correspond à une zéro (un X-interception) dans un intervalle de la courbe de son dérivé qui traverse la X-axe passant vers le bas (comme en (2, 0)).

Sur un graphique dérivé, vous'avons obtenu une m-axe. Lorsque vous êtes à la recherche à différents points sur le graphique dérivé, ne pas oublier que le y-coordonner d'un point, comme (2, 0), sur un graphique d'une première dérivée vous le dit pente de la fonction d'origine, et non sa hauteur. Pensez à la y-sur le premier axe graphe dérivé en tant que pente-ou l'axe m-axis- vous pourriez penser de points généraux sur le premier graphique dérivé comme ayant des coordonnées (X, m).

• 
  
  
  
  

  UN décroissante sur un intervalle correspondant à une fonction négatif intervalle sur le graphe de la dérivée (ou zéro pour un seul point si la fonction a un point d'inflexion horizontal). L'intervalle négatif sur le graphique dérivé est en dessous de la X-axe (ou dans le cas d'un point d'inflexion horizontal, le graphique dérivé touche le X-axe à un seul point). Voir intervalles B, C, D, et E dans la figure (mais les considérer comme une seule section), où F descend tout le chemin de l'max locale (-2, 64) à la min locale (2, -64) et où

  

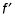
  est négative entre (-2, 0) et (2, 0), sauf pour au point (0, 0) sur

  

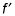
  qui correspond au point d'inflexion horizontal sur F.

• Une locale min sur le graphique d'une fonction correspond à un zéro (e X-interception) dans un intervalle de la courbe de son dérivé qui traverse la X-axe de monter (comme en (2, 0)).

Prenons maintenant un second voyage le long F de considérer ses intervalles de concavité et de ses points d'inflexion. Considérons d'abord les intervalles A et B sur la figure. Le graphique de la F est en baisse concave - ce qui signifie la même chose que d'un décroissante pente - jusqu'à ce qu'il arrive au point d'inflexion à environ (-1,4, 39,6).

Ainsi, le graphe de

diminue jusqu'au fond à environ (-1,4, -60). Ces coordonnées vous diront que le point d'inflexion à -1,4 sur F a une pente de -60. Notez que le point d'inflexion sur F au (-1,4, 39,6) est le point le plus raide sur ce tronçon de la fonction, mais il a le plus petit pente parce que sa pente est un plus grand négatif que la pente à tout autre point à proximité.

Entre (-1,4, 39,6) et le prochain point d'inflexion (0, 0), F est concave vers le haut, ce qui signifie la même chose que d'un croissant pente. Ainsi le graphique de

augmente d'environ -1,4 à l'endroit où il touche un maximum locale à (0, 0). Voir intervalle C dans la figure. Prenons une pause ce voyage pour certains plus de règles.

• Un concave vers le bas intervalle sur le graphique d'une fonction correspondant à une décroissante intervalle sur le graphique de ses dérivés (intervalles A, B, et D dans la figure). Et une concave en haut intervalle sur la fonction correspond à un croissant intervalle sur les intervalles dérivés (C, E, et F).

• Un point d'inflexion sur une fonction (sauf pour un point d'inflexion verticale où le dérivé est undefined) correspond à une extremum local sur le graphique de son dérivé. Un point d'inflexion de la minimum pente (dans son voisinage) correspond à une section locale min sur le dérivé graph- un point d'inflexion de la maximum pente (dans son voisinage) correspond à une section locale max sur le graphique dérivé.

Reprise de votre voyage, après (0, 0), F est concave vers le bas jusqu'à ce que le point d'inflexion à environ (-1,4, 39,6) - cela correspond à la section décroissante de

à partir de (0, 0) de sa min à (1,4, -60) (D intervalle sur la figure). Finalement, F est concave vers le haut le reste de la voie, qui correspond à la partie croissante de

à partir de (1.4, -60) (intervalles E et F dans la figure).

Eh bien, que vous apporte à peu près à la fin de la route. Des allers-retours entre les graphes d'une fonction et son dérivé peut être très essayer d'abord. Si votre tête commence à tourner, prendre une pause et de revenir à ce genre de choses plus tard.

Maintenant, regardez à nouveau le graphique de la dérivée,

dans la figure et aussi le signe graphique pour

dans la figure suivante.

Ce signe graphique, car il est un deuxième signe dérivé graphique, porte exactement (bien, presque exactement) la même relation avec le graphique de

comme une première dérivée ours signe graphique au graphique d'une fonction régulière. Autrement dit, négatif intervalles sur le signe graphique dans la figure

vous montrer où le graphique de

est décroissante- positif intervalles sur le signe graphique

vous montrer où

est croissant. Et les points où les signes basculer du positif au négatif ou vice-versa

vous montrer où

a extrema locaux.