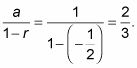Comment analyser la convergence absolue et conditionnelle
Beaucoup de séries divergentes des termes positifs convergent si vous modifiez les signes de leurs conditions afin qu'ils alternent entre positif et négatif. Par exemple, vous savez que la série harmonique diverge:
Mais, si vous changez tout autre signe négatif, vous obtenez le série harmonique alternée, qui converge:
Par ailleurs, cette série converge vers ln 2, ce qui équivaut à environ 0,6931.
Une série alternée est dit être conditionnellement convergente si elle est convergente comme il est, mais deviendrait divergente si toutes ses conditions ont été positifs. Une série alternée est dit être absolument convergente si elle serait convergente même si toutes ses conditions ont été positifs. Et une telle série absolument convergente est également automatiquement convergente comme il est.
Voici un exemple. Déterminer la convergence ou la divergence de la série alternée suivant:
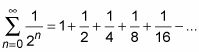
Si tous ces termes sont positifs, vous auriez la série géométrique familière,
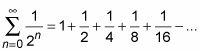
qui, par la règle de série géométrique, converge vers 2. Parce que la série converge positif, la série alternée doit également converger et vous dire que la série alternée est absolument convergente.
Le fait que la convergence absolue implique la convergence ordinaire est juste du bon sens si vous pensez à ce sujet. La précédente série géométrique de termes positifs converge vers 2. Si vous avez fait tous les termes négatifs, il serait résumé à -2, à droite? Donc, si certains des termes sont positifs et d'autres négatifs, la série doit converger vers quelque chose entre -2 et 2.
Avez-vous remarqué que la série alternée ci-dessus est une série géométrique tel quel avec
(Rappelons que la formule pour la somme d'une série géométrique fonctionne à chaque fois r est comprise entre -1 et 1- cela fonctionne ainsi pour la série en alternance ainsi que pour la série positive) La formule donne sa somme.:
-
Ports série de votre PC -
Graphique sommes partielles d'une série infinie sur la TI-84 Plus -
Calcul classeur pour les nuls -
En comparant les séquences divergent et convergent -
Connexion d'un série avec ses deux séquences apparentées -
Déterminer si une série converge à l'aide du test de comparaison solidaire
Déterminer si une série de Taylor est convergente ou divergente Parce que la série de Taylor est une forme de séries de puissance, chaque série de Taylor a aussi un intervalle de convergence. Lorsque cet intervalle est l'ensemble des nombres réels, vous pouvez utiliser la série pour trouver la valeur de…
Exprimer et se rapprochant de fonctions en utilisant la série de Taylor Il est important de comprendre la différence entre expressing une fonction comme une série infinie et unpproximating une fonction en utilisant un nombre fini de termes de la série. Vous pouvez penser à une série de puissance comme un polynôme…
Exprimant la fonction sin x comme une série Si vous voulez trouver la valeur approximative du péché X, vous pouvez utiliser une formule pour l'exprimer comme une série. Cette formule exprime la fonction sinus comme une série alternée:Pour donner un sens à cette formule, utilisez la…
Comment analyser une série télescopique Vous ne voyez pas beaucoup de séries de télescopage, mais la règle de série télescopique est un bon à garder dans votre sac à malices - vous ne savez jamais quand il pourrait venir dans maniable. Considérons la série suivante:Pour voir que…
Comment analyser un p-series Soi-disant p-séries sont des séries relativement simple, mais important, que vous pouvez utiliser comme points de référence pour déterminer la convergence ou la divergence des séries plus compliqué. UN p-série est de la forme(où p est un…
Comment déterminer si une série alternée converge ou diverge Un alternatif série est une série où les termes alternent entre positif et négatif. Vous pouvez dire que une série alternée converge si deux conditions sont remplies:C'est ne terme converge vers zéro.Ses termes sont non-augmentation - en…
Comment reconnaître un p-series Un type important de série est appelé le p-série. UN p-série peut être convergent ou divergent, en fonction de sa valeur. Il prend la forme suivante:Voici un exemple d'une commune p-série, lorsque p = 2:Voici quelques autres exemples de…
Comment faire pour tester si une série converge ou diverge Dites que vous êtes à essayer de comprendre si une série converge ou diverge, mais il ne correspond à aucune des épreuves que vous connaissez. Pas de soucis. Vous trouverez une série de référence que vous savez converge ou diverge puis…
Comment utiliser le test de comparaison de limite pour déterminer si une série converge L'idée derrière le test de comparaison limite est que si vous prenez une série convergente connu et multipliez chacun de ses termes par un nombre, alors que la nouvelle série converge également. Et il n'a pas d'importance si le multiplicateur…
Comment utiliser le test de nième terme pour déterminer si une série converge Si les termes individuels d'une série (en d'autres mots, les termes de séquence sous-jacente de la série) ne convergent pas vers zéro, alors la série doit diverger. C'est le ne test de terme pour divergence. Cela est généralement un très…
Comment utiliser le test de racine pour déterminer si une série converge Le test de racine ne se compare pas une nouvelle série à une série de référence connu. Il fonctionne en ne regardant que la nature de la série que vous essayez de comprendre. Vous utilisez le test de racine d'enquêter sur la limite de la ne…
Comment travailler avec des séries géométrique Série géométrique sont des séries relativement simple, mais important, que vous pouvez utiliser comme points de référence pour déterminer la convergence ou la divergence des séries plus compliqué. Une série géométrique est une série de…
Théorie des perturbations: la méthode d'approximation de la théorie des cordes Les équations de la théorie des cordes sont incroyablement complexes, si bien qu'elles ne peuvent être résolus grâce à une méthode mathématique d'approximation appelé la théorie des perturbations. Cette méthode est utilisée en mécanique…
Préparation ASVAB: nombres positifs et négatifs Assurez-vous que vous êtes familier avec travailler avec des chiffres positifs et négatifs pour la ASVAB. Les nombres peuvent être positifs ou négatifs. Un nombre positif est un nombre supérieur à zéro. Donc 4- 3.2- 793- 3 / 4- 1 / 2- et 430…