Comment calculer les sorties pour les fonctions rationnelles
En pré-calcul, vous pouvez calculer sorties pour les fonctions rationnelles. UN fonction rationnelle est une fonction qui peut être exprimé comme le quotient de deux polynômes, de telle sorte que
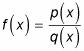
où le degré de q(X) Est supérieure à zéro.
Voici les étapes à suivre pour trouver les sorties (et finalement graphiquement) fonctions rationnelles:
Rechercher asymptotes verticales.
Avoir la variable sur le fond d'une fraction est un problème, car le dénominateur d'une fraction ne peut jamais être égal à zéro. Habituellement, une certaine valeur (s) de domaine X rend le dénominateur zéro. Si il existe un X-valeur qui rend le dénominateur zéro, mais pas le numérateur, alors le graphe a ce qu'on appelle un asymptote verticale à ceci X-valeur. Graphes de l'asymptote verticale d'abord vous indique le nombre dans le domaine où votre graphique ne peut pas passer à travers. Le graphique se rapproche de ce point, mais ne l'atteint jamais. Avec cela à l'esprit, quelle valeur (s) pour X peux tu pas brancher dans la fonction rationnelle?
Les fonctions suivantes sont toutes rationnelle:
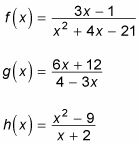
Essayez de trouver la valeur de X dans lequel la fonction est indéfini. Utilisez les étapes suivantes pour trouver l'asymptote verticale pour F(X) premier:
Réglez le dénominateur de la fonction rationnelle égal à zéro.
Pour F(X), X2 + 4X - 21 = 0.
Résolvez cette équation pour X.
Parce que cette équation est quadratique, essayez de factoriser. Cette facteurs quadratique (X + 7)(X - 3) = 0. Set chaque facteur égal à zéro à résoudre. Si X + 7 = 0, X = -7. Si X - 3 = 0, X = 3. Vos deux asymptotes verticales, par conséquent, sont X = -7 Et X = 3, comme représenté sur la figure.
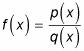
Maintenant vous pouvez trouver l'asymptote verticale pour g(X). Suivez la même série d'étapes:
4 - 3X = 0
X = 4/3
Maintenant vous avez votre asymptote verticale pour g(X). C'était facile! Le temps de faire tout cela de nouveau pour h(X):
X + 2 = 0
X = -2
Gardez ces équations pour les asymptotes verticales ferment par parce que vous en aurez besoin plus tard lors de la représentation.
Recherchez asymptotes horizontales.
Pour trouver une asymptote horizontale d'une fonction rationnelle, vous devez regarder le degré des polynômes dans le numérateur et le dénominateur. La degré est la plus haute puissance de la variable dans l'expression polynomiale. Voici comment procéder:
Si le dénominateur a le plus grand degré (comme dans le F(X) Exemple à l'étape 1), l'asymptote horizontale est automatiquement la X-axe, ou y = 0.
Si le numérateur et le dénominateur ont un degré égal, vous devez diviser les coefficients principaux (les coefficients des termes avec les plus hauts degrés) pour constater l'asymptote horizontale.
Si les termes avec les plus hauts degrés ne sont pas écrites dans le premier polynôme, vous pouvez réécrire les deux polynômes de sorte que les plus hauts degrés viennent en premier. Par exemple, vous pouvez réécrire le dénominateur g(X) Comme -3X + 4 de sorte qu'il apparaît dans l'ordre décroissant.
La fonction g(X) A degrés égaux en haut et en bas. Pour trouver l'asymptote horizontale, diviser les grands coefficients des termes plus haut degré:
Vous avez maintenant votre asymptote horizontale pour g(X). Accrochez-vous à cette équation pour la représentation graphique!
Si le numérateur a le plus grand degré d'exactement un de plus que le dénominateur, le graphique aura une oblique asymptote- voir l'étape 3 pour plus d'informations sur la façon de procéder.
Cherchez asymptotes obliques.
Asymptotes obliques ne sont ni horizontale ni verticale. En fait, une asymptote n'a même pas à être une ligne droite au tout-cela peut être une légère courbe ou une courbe vraiment compliqué.
Pour trouver une asymptote oblique, vous devez utiliser la longue division de polynômes pour trouver le quotient. Vous prenez le dénominateur de la fonction rationnelle et divisez-le dans le numérateur. Le quotient (en négligeant le reste) vous donne l'équation de la ligne de votre asymptote oblique.
Vous devez comprendre la longue division de polynômes afin de compléter le graphique d'une fonction rationnelle avec une asymptote oblique.
La h(X) Exemple de l'étape 1 a une asymptote oblique car le numérateur a le plus haut degré dans le polynôme. En utilisant la division de long, vous obtenez un quotient de X - 2. Ce quotient signifie l'asymptote oblique suit l'équation y = X - 2. Parce que cette équation est au premier degré, graphique, il vous en utilisant le forme d'une pente. Gardez cette asymptote oblique à l'esprit, parce graphique est à venir jusqu'à!
Localisez le X- et y-interceptions.
La dernière pièce du puzzle est de trouver les intersections (où la ligne ou la courbe traverse la X- et y-axes) de la fonction rationnelle, si elles existent:
Pour trouver le y-interception d'une équation, réglez X = 0. (Branchez 0 partout où vous voyez X.) La y-interception de F(X) De l'étape 1, par exemple, est 21/01.
Pour trouver le X-interception d'une équation, réglez y = 0 et à résoudre pour X.
Pour toute fonction rationnelle, le raccourci pour trouver le X-interception est de mettre le numérateur égal à zéro, puis résoudre. Parfois, quand vous faites cela, cependant, l'équation que vous obtenez est insoluble, ce qui signifie que la fonction rationnelle ne dispose pas d'une X-interception.
La X-interception de F(X) Est 3.1.
Cette figure montre le graphique pour F(X).
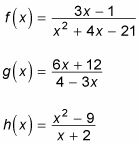
Maintenant trouver les interceptions pour g(X) Et h(X) De l'étape 1. Ce faisant, vous trouverez les points suivants:
g(X) a un y-interception à 3 et un X-intercepter à -2.
h(X) a un y-interception à -9/2 et X-intercepte à
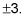
Voici le graphe pour g(X):
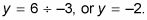
Voici le graphe pour h(X):
Comment représenter graphiquement et de transformer une fonction exponentielle Représentation graphique d'une fonction exponentielle est utile lorsque vous souhaitez analyser visuellement la fonction. Cela vous permet de voir vraiment la croissance ou la décroissance de ce que vous avez à faire. La fonction de parent de…
Comment tracer une fonction rationnelle quand le numérateur a le plus haut degré Fonctions rationnelles où le numérateur a le plus grand degré ne sont pas réellement asymptotes horizontales. Au lieu de cela, ils ont asymptotes obliques que vous trouvez en utilisant la longue division.Par exemple, un graphique h (X):Dessinez…
Comment tracer une fonction rationnelle avec dénominateur ayant le plus haut degré Après vous calculez tous les asymptotes et la X- et y-intercepte pour une fonction rationnelle, vous avez toutes les informations dont vous avez besoin pour commencer graphiquement la fonction. En tout état de fonction rationnelle où le…
Comment tracer une fonction rationnelle avec numérateur ayant le plus haut degré Après vous calculez tous les asymptotes et la X- et y-intercepte pour une fonction rationnelle, vous avez toutes les informations dont vous avez besoin pour commencer graphiquement la fonction. Fonctions rationnelles où le numérateur a le plus…
Comment tracer une fonction sécante Vous pouvez représenter graphiquement une fonction sécante F(X) = S X en utilisant des mesures similaires à celles de la tangente et cotangente. Comme tangente et cotangente, le graphique de la sécante a asymptotes. En effet, la sécante est…
Comment tracer une fonction rationnelle avec numérateur et le dénominateur des degrés égaux Après vous calculez tous les asymptotes et la X- et y-intercepte pour une fonction rationnelle, vous avez toutes les informations dont vous avez besoin pour commencer graphiquement la fonction. Fonctions rationnelles avec des degrés égaux dans le…
Comment tracer une fonction tangente La fonction tangente a un graphique de parent comme toute autre fonction. L'aide du graphique de cette fonction, vous pouvez faire le même type de transformation qui applique le graphique parent de toute fonction. La meilleure façon de se rappeler…
Comment représenter graphiquement des fonctions parentales et les journaux transformées Vous voulez quelques bonnes nouvelles, gratuitement? Représentation graphique des fonctions parentales et les journaux transformées est un clin d'oeil! Vous pouvez modifier n'importe quel journal dans une expression exponentielle, de sorte que…
Comment intégrer à l'aide de fractions partielles lorsque le dénominateur ne contient que des facteurs linéaires Vous pouvez utiliser la méthode des fractions partielles d'intégrer des fonctions rationnelles (Rappelons qu'une fonction rationnelle est un polynôme divisé par un autre.) L'idée de base derrière l'approche de fraction partielle est “…
Comment résoudre intégrales impropres pour les fonctions qui ont asymptotes verticales Vous résolvez intégrales impropres en les transformant en des problèmes de limites. Vous ne pouvez pas leur faire de la manière habituelle. Voici comment vous résoudre intégrales impropres pour les fonctions qui ont asymptotes verticales. Il…
Comment résoudre limites à l'infini en utilisant asymptotes horizontales Asymptotes horizontales et les limites à l'infini vont toujours main dans la main. Vous ne pouvez pas avoir l'un sans l'autre. Si vous avez une fonction rationnelle commedéterminer la limite à l'infini ou infini négatif est le même que de…
Polynômes et pré-calcul Fonctions polynômes ont graphiques qui sont des courbes lisses. Ils vont de l'infini négatif à l'infini positif dans une belle, de la mode qui coule sans brusques changements de direction. Pièces de fonctions polynômes sont utiles lors de la…
Graphique sécante et fonctions cosécantes Les graphiques des fonctions de cosécantes sécantes et Inverse Inverse faudra un peu expliquer. Premièrement, gardez à l'esprit que les fonctions sécantes et cosécantes ne possèdent pas toutes les valeurs de sortie (y-valeurs) entre -1 et 1,…
Graphiquement l'asymptote d'une fonction tangente Un asymptote est une ligne qui contribue à donner sens à un graphique d'une fonction de la trigonométrie. Cette ligne ne fait pas partie de la graph- de la fonction plutôt, il permet de déterminer la forme de la courbe en montrant où la courbe…