Comment trouver la valeur moyenne avec le théorème de la valeur moyenne pour les intégrales
Vous pouvez trouver la valeur moyenne d'une fonction sur un intervalle fermé en utilisant le théorème de la moyenne pour les intégrales. La meilleure façon de comprendre le théorème de la valeur moyenne pour les intégrales est avec un schéma - regardez la figure suivante.
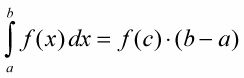
Le graphique de gauche montre un rectangle dont la surface est clairement Moins que l'aire sous la courbe entre 2 et 5. Ce rectangle a une hauteur égale à la plus faible sur le point de la courbe dans l'intervalle de 2 à 5.
Le graphique du milieu montre un rectangle dont la hauteur est égale à la point de la courbe la plus élevée. Sa superficie est clairement plus grand que l'aire sous la courbe. A présent, vous pensez, “ est pas là un rectangle plus grand que la courte et plus courte que la hauteur d'un dont la superficie est le même que l'aire sous la courbe ”?; Bien sûr. Et ce rectangle traverse évidemment la courbe quelque part dans l'intervalle. Ce soi-disant rectangle de valeur moyenne, montré sur la droite, résume essentiellement le théorème Valeur moyenne pour les intégrales.
Il est vraiment juste du bon sens. Mais voici le charabia.
Le théorème de la valeur moyenne pour les intégrales: Si F (X) Est une fonction continue sur l'intervalle fermé [a, b], Alors il existe un certain nombre c dans l'intervalle fermé de telle sorte que
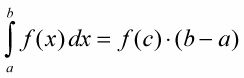
Le théorème essentiellement garantit simplement l'existence de la valeur moyenne rectangle.
La superficie de la valeur moyenne rectangle - qui est la même que l'aire sous la courbe - equals longueur fois largeur, ou base fois hauteur, droit?
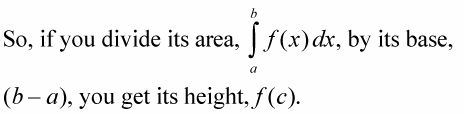
Cette hauteur est la valeur moyenne de la fonction sur l'intervalle en question.
Voici un exemple. Quelle est la vitesse moyenne d'une voiture entre t = 9 secondes et t = 16 secondes dont la vitesse dans pieds en soicond est donnée par la fonction,
Selon la définition de la valeur moyenne, cette vitesse moyenne est donnée par
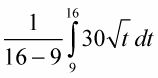
Déterminer l'aire sous la courbe entre 9 et 16.
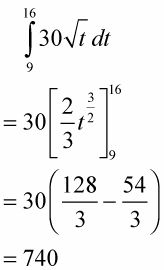
Cette zone, en passant, est la distance totale parcourue de 9 à 16 secondes. Voyez-vous pourquoi? Considérez le rectangle de la valeur moyenne pour ce problème. Sa hauteur est une vitesse (parce que les valeurs de la fonction, ou les hauteurs, sont des vitesses) et sa base est un laps de temps, de sorte que sa superficie est vitesse fois temps ce qui équivaut distance. Sinon, rappelons que le dérivé de la position est la vitesse. Donc, la primitive de vitesse - ce que vous venez de faire à cette étape - est la position, et le changement de position de 9 à 16 secondes donne la distance totale parcourue.
Divisez cette zone, la distance totale, par l'intervalle de temps du 9 au 16, à savoir 7.
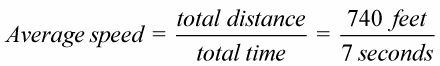
# 8776- 105,7 pieds par seconde
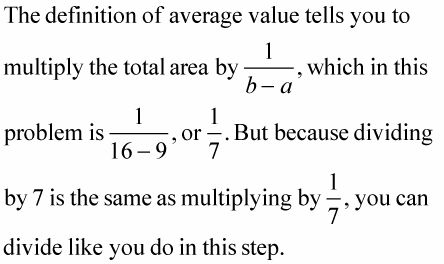
Il est plus logique de penser à ces problèmes en termes de division: région égal à égal base fois hauteur, si la hauteur du rectangle est égale à la valeur moyenne de sa surface divisé par sa base.
-
Comment tracer une valeur sur un histogramme TI-Nspire -
Comment mesurer triangles -
10 choses à retenir sur l'intégration et le calcul -
Comment fonctionne l'intégration: il est juste plus de fantaisie -
Comment la fonction de zone fonctionne -
Comment analyser position, la vitesse et l'accélération de la différenciation
Comment zone avec des rectangles médianes rapprocher Une bonne façon de se rapprocher des zones avec des rectangles est de faire de chaque rectangle traverser la courbe au milieu de côté supérieur de ce rectangle. Une somme milieu est une bien meilleure estimation de la superficie que ce soit à…
Comment rapprocher zone avec la règle du trapèze Avec la règle, à la place de la zone approximation en utilisant des rectangles (comme vous le faites avec la gauche, à droite, et les méthodes de rectangle médianes), vous superficie approximative avec trapèze - pouvez-vous deviner? -…
Comment calculer la vitesse instantanée avec des limites Vous pouvez calculer la vitesse instantanée d'un objet en utilisant des limites. Dites que vous et votre chat de calcul épris êtes accroché un jour, et que vous décidez de laisser tomber une balle hors de votre fenêtre du deuxième étage.…
Comment déterminer les vitesses maximum et minimum d'objets en mouvement L'une des utilisations les plus pratiques de différenciation est de trouver les valeurs maximales ou minimales d'une fonction dans le monde réel, par exemple, la vitesse minimale d'un objet en mouvement et maximum.Vous pouvez penser vitesse que la…
Comment trouver la valeur moyenne d'une fonction avec le théorème de la valeur moyenne pour les intégrales Vous pouvez trouver la valeur moyenne d'une fonction sur un intervalle fermé en utilisant le théorème de la moyenne pour les intégrales. La meilleure façon de comprendre le théorème de la moyenne est d'un diagramme - check it out…
Comment trouver la zone entre deux courbes Pour trouver la zone entre deux courbes, vous devez venir avec une expression pour un rectangle étroit qui se trouve sur l'une courbe et monte à l'autre.de X = 0 et X = 1:Pour obtenir la hauteur du rectangle représentant dans la figure,…
Comment mesurer les vestiaires sous une courbe Vous pouvez utiliser une fonction de la zone pour mesurer la surface sous une courbe, alors même que les changements de la région. Par exemple, disons que vous avez une fonction ancienne, F (t). Imaginez que, à un t-valeur, appeler s, vous tracez…
Calculer rapidement intégrales définies en utilisant le théorème fondamental Voici un théorème d'intégration de raccourci super-duper que vous allez utiliser pour le reste de vos jours naturels nés - ou tout au moins jusqu'à la fin de votre séjour avec calcul. Cette méthode de raccourci est tout ce que vous avez…
Le théorème fondamental du calcul Le théorème fondamental du calcul est l'un des théorèmes les plus importants dans l'histoire des mathématiques. Il précise que, compte tenu d'une fonction de la zone UNF qui balaie la zone sous F (t),la vitesse à laquelle zone est balayée…
Comment calculer l'aire d'un parallélogramme, cerf-volant, ou trapézoïdale Les formules de la zone de parallélogramme, cerf-volant, et trapèze sont basés sur l'aire d'un rectangle. Les chiffres suivants montrent comment chacun de ces trois quadrilatères se rapporte à un rectangle, et la liste suivante vous donne les…
Comment représenter graphiquement la distribution uniforme La distribution uniforme est une distribution continue qui affecte seulement probabilités positives au sein d'un intervalle spécifié (un, b) - Qui est, toutes les valeurs entre un et b. (un et b sont deux constants- ils peuvent être négatifs ou…
L'écart type, la variance et coefficient de variation des données de biostatistique La écart-type (généralement abrégé SD, sd, ou juste s) D'un tas de chiffres vous indique combien les numéros individuels ont tendance à différer (dans les deux sens) de la moyenne. Il est calculé comme suit:Cette formule est dit que vous…
Calcul de la vitesse moyenne sur la base de la distance et du temps En physique, la vitesse moyenne est la distance totale vous voyagez divisé par le temps total nécessaire. La vitesse est représentée par la variable v, et la vitesse moyenne est parfois écrit commeUne barre sur une variable signifie la moyenne…
Physique - déplacement et la vitesse Imaginez que la voiture commence voyageant le long d'une route après le démarrage à partir d'un panneau spécifique. Pour connaître la position exacte de la voiture après qu'il a parcouru une distance donnée, vous avez besoin de connaître non…