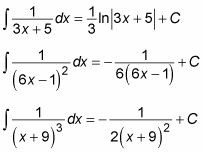Mise en place des fractions partielles quand vous avez des facteurs linéaires distinctes
Votre première étape de tout problème qui implique fractions partielles est de reconnaître ce cas, vous avez affaire à de sorte que vous pouvez résoudre le problème. Le cas le plus simple dans lequel les fractions partielles sont utiles est lorsque le dénominateur est le produit de distinct facteurs linéaires - à savoir, les facteurs linéaires qui sont non répétitif.
Par exemple, vous pouvez changer cela:
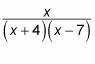
pour ça:
Gardez à l'esprit que pour chaque facteur linéaire distincte dans le dénominateur, vous devez ajouter une fraction partielle de la forme suivante:
Par exemple, supposons que vous souhaitez intégrer l'expression rationnelle suivante:
Le dénominateur est le produit de trois facteurs distincts linéaires - X, (X + 2), et (X - 5) - il est donc égale à la somme de trois fractions avec des dénominateurs ces facteurs que:
Le nombre de facteurs linéaires distinctes dans le dénominateur de l'expression originale détermine le nombre de fractions partielles. Dans cet exemple, la présence de trois éléments dans le dénominateur de l'expression originale donne trois fractions partielles.
Vous avez deux façons de trouver les inconnues dans une somme de fractions partielles. Le moyen facile et rapide est d'utiliser les racines de polynômes. Malheureusement, cette méthode ne trouve pas toujours toutes les inconnues dans un problème, mais il trouve souvent quelques-uns d'entre eux. La deuxième façon est de mettre en place un système d'équations.
Quand une somme de fractions partielles a facteurs linéaires distinctes, vous pouvez utiliser les racines de ces facteurs linéaires pour trouver les valeurs d'inconnues:
Pour trouver les valeurs des inconnues UN, B, et C, d'abord obtenir un dénominateur commun sur le côté droit de cette équation (le même dénominateur qui est sur le côté gauche):
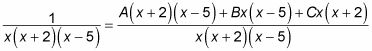
Maintenant, multipliez deux côtés par ce dénominateur:
1 = UN(X + 2) (X - 5) + Bx(X - 5) + Cx(X + 2)
Pour trouver les valeurs de UN, B, et C, remplacer les racines des trois facteurs (0, -2, et 5):
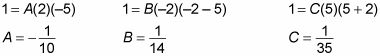
Brancher ces valeurs dans l'équation originale vous donne:
Cette expression est équivalente à ce que vous avez commencé avec, mais il est beaucoup plus facile à intégrer. Pour ce faire, utilisez la règle Somme pour la diviser en trois intégrales, la règle multiple constant de se déplacer en dehors des coefficients fractionnaires chaque substitution intégrante, et variable de faire l'intégration. Voici la réponse de sorte que vous pouvez essayer:
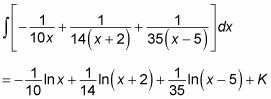
Cette réponse utilise K plutôt que C pour représenter la constante d'intégration pour éviter toute confusion, parce que vous avez déjà utilisé C dans les fractions partielles précédentes.
Lorsque vous démarrez avec un facteur linéaire distincte, en utilisant des fractions partielles vous laisse avec une intégrale sous la forme suivante:
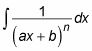
Intégrer l'aide de la substitution de variable u = hache + b de sorte que dx = a du et
Cette substitution donne l'intégrale suivante:
Voici quelques exemples:
-
Comment changer les fractions impropres et des nombres fractionnaires -
Comment créer des fractions équivalentes en utilisant des dénominateurs communs -
Comment réduire les fractions en utilisant factorisation -
Des conseils de base en mathématiques: fractions -
Comment ajouter des fractions avec des dénominateurs communs -
Comment trouver la somme de fractions avec le même dénominateur
Comment multiplier deux fractions et de réduire la réponse Pour multiplier deux fractions, vous devez avoir une connaissance de base de la table de multiplication et de la capacité de réduire la réponse à sa plus simple expression.Multiplier les numérateurs (Les numéros sur le dessus) ensemble pour…
Comment soustraire des fractions avec le même dénominateur Soustraction de fractions avec le même dénominateur (chiffre du bas) est facile. Quand les dénominateurs sont les mêmes, vous pouvez simplement que des fractions que des morceaux de gâteau.Pour soustraire une fraction d'un autre quand ils ont…
Comment soustraire des fractions avec des dénominateurs communs Comme avec addition, soustraction de fractions ayant le même dénominateur (également appelée dénominateur commun) Est très simple: Il suffit de soustraire le second numérateur de la première et de garder le même dénominateur. Dans certains…
Comment décomposer fractions partielles Un processus appelé fractions partielles prend une fraction et exprime comme la somme ou la différence des deux autres fractions. Dans le calcul, ce processus est utile avant d'intégrer une fonction. Parce que l'intégration est tellement plus…
Décomposer fractions partielles en 8 étapes Lorsque votre pré-calcul instructeur vous demande de décomposer fractions partielles, il est en fait pas aussi salissant que ça sonne. Le processus de décomposition d'une fraction partielle vous oblige à séparer la fraction en deux (ou parfois…
Comment distinguer les expressions rationnelles corrects et incorrects Intégration par fractions partielles fonctionne uniquement avec expressions rationnelles appropriées, mais pas avec expressions rationnelles inappropriées. Raconter une fraction propre d'une mauvaise ci est facile: Une fraction a / b est correcte…
Comment intégrer à l'aide de fractions partielles lorsque le dénominateur ne contient que des facteurs linéaires Vous pouvez utiliser la méthode des fractions partielles d'intégrer des fonctions rationnelles (Rappelons qu'une fonction rationnelle est un polynôme divisé par un autre.) L'idée de base derrière l'approche de fraction partielle est “…
L'intégration en utilisant des fractions partielles lorsque le dénominateur contient des facteurs quadratiques irréductibles Vous pouvez utiliser la méthode des fractions partielles d'intégrer des fonctions rationnelles, y compris les fonctions ayant des dénominateurs communs qui contiennent irréductible facteurs quadratiques (qui est, les facteurs du second degré…
Intégrer les fonctions où le dénominateur contient facteurs quadratiques irréductibles Parfois, vous ne pouvez pas le facteur A dénominateur tout le chemin à des facteurs linéaires parce que certaines équations du second degré sont irréductibles - comme les nombres premiers, ils ne peuvent pas être pris en compte.Vérifier la…
Mise en place des fractions partielles lorsque vous avez répété facteurs linéaires Votre première étape de tout problème qui implique fractions partielles est de reconnaître ce cas, vous avez affaire à de sorte que vous pouvez résoudre le problème. Un cas où vous pouvez utiliser des fractions partielles est avec des…
Mise en place des fractions partielles lorsque vous avez répété facteurs quadratiques Votre première étape de tout problème qui implique fractions partielles est de reconnaître ce cas, vous avez affaire à de sorte que vous pouvez résoudre le problème. Un cas où vous pouvez utiliser des fractions partielles est avec facteurs…
Mise en place des fractions partielles quand vous avez des facteurs distincts Votre première étape de tout problème qui implique fractions partielles est de reconnaître ce cas, vous avez affaire à de sorte que vous pouvez résoudre le problème. Un cas où vous pouvez utiliser des fractions partielles est lorsque le…
Préparation ASVAB: comment ajouter et soustraire des fractions Additionner et soustraire des fractions pour la ASVAB (ou à d'autres fins) peut être aussi simple que de multiplier et diviser entre eux, ou bien il peut être plus difficile. Comme les informations ci-dessous montre, tout dépend si les fractions…
Préparation ASVAB: comment simplifier fractions Simplifier (ou la réduction) des fractions signifie faire de la fraction la plus simple possible. Vous êtes généralement tenu pour simplifier fractions sur les sous-tests de mathématiques ASVAB avant de pouvoir sélectionner la bonne…