Mise en place des fractions partielles quand vous avez des facteurs distincts

Votre première étape de tout problème qui implique fractions partielles est de reconnaître ce cas, vous avez affaire à de sorte que vous pouvez résoudre le problème. Un cas où vous pouvez utiliser des fractions partielles est lorsque le dénominateur est le produit de distinct

facteurs quadratiques - qui est, les facteurs du second degré qui sont non répétitif.

Pour chaque facteur quadratique distincte dans le dénominateur, ajouter une fraction partielle de la forme suivante:

Par exemple, supposons que vous souhaitez intégrer cette fonction:

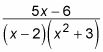
Le premier facteur dans le dénominateur est linéaire, mais le second est quadratique et ne peut pas être décomposée à des facteurs linéaires. Donc, mettre en place vos fractions partielles comme suit:

Le nombre de facteurs quadratiques distinctes dans le dénominateur vous indique combien de fractions partielle que vous obtenez. Donc, dans cet exemple, deux facteurs dans le dénominateur donnent deux fractions partielles.

Travailler systématiquement avec un système d'équations

Mise en place d'un système d'équations est une méthode alternative pour trouver la valeur d'inconnues lorsque vous travaillez avec des fractions partielles. Il est pas aussi simple que de brancher dans les racines de facteurs, mais il est votre seule option lorsque la racine d'un facteur quadratique est imaginaire.

Voici un problème pour illustrer cette méthode:

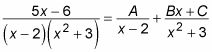
Pour commencer, de voir jusqu'où vous pouvez obtenir en branchant les racines des équations. Commencez par obtenir un dénominateur commun sur le côté droit de l'équation:

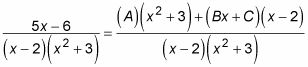
Maintenant, multipliez toute l'équation par le dénominateur:

5X - 6 = (UN) (X² + 3) + (Bx + C) (X - 2)

La racine de X - 2 est 2, nous allons X = 2 et voyez ce que vous obtenez:

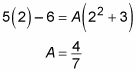
Maintenant, vous pouvez remplacer

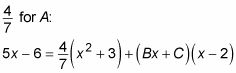
Malheureusement, X² + 3 n'a pas de racine dans les nombres réels, de sorte que vous besoin d'une approche différente. Tout d'abord, se débarrasser des parenthèses sur le côté droit de l'équation:

Ensuite, combiner des termes similaires (à l'aide X comme variable par lequel vous jugez similitude). Ceci est juste l'algèbre:

Parce que cette équation fonctionne pour tous les valeurs de X, vous prenez maintenant ce qui semble être une étape douteuse, brisant cette équation en trois équations distinctes comme suit:

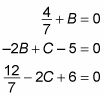
À ce stade, un peu d'algèbre vous dit que

Ainsi, vous pouvez remplacer les valeurs de UN, B, et C Retour dans les fractions partielles:

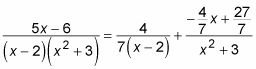
Vous pouvez simplifier la deuxième fraction un peu:

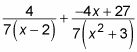
Facteurs quadratique de la forme (hache² + C)

Lorsque vous commencez avec un facteur quadratique de la forme (hache² + C), En utilisant des fractions partielles se traduit par les deux intégrales suivantes:

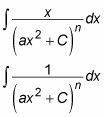
Intégrer le premier en utilisant la substitution de variable u = hache² + C de sorte que du = 2hache dx et

Cette substitution donne l'intégrale suivante:

Voici quelques exemples:

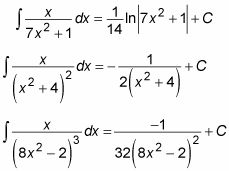
Pour évaluer la seconde intégrale, utilisez la formule suivante:

Facteurs quadratique de la forme (hache² + bx + C)

La plupart des professeurs de mathématiques ont au moins une once de pitié dans leurs coeurs, afin qu'ils ne tendent pas à vous donner des problèmes qui comprennent ce cas le plus difficile. Lorsque vous commencez avec un facteur quadratique de la forme (hache² + bx + C), En utilisant des fractions partielles se traduit par l'intégrale suivante:

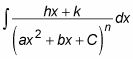
D'accord, ça beaucoup trop de lettres et pas assez numéros. Voici un exemple:

Ceci est à propos de l'intégrale plus poilu que vous allez jamais de voir à l'extrémité d'une fraction partielle. Pour l'évaluer, vous souhaitez utiliser la substitution de variable u = X² + 6X + 13 de sorte que du = (2X + 6) dx. Si le numérateur étaient 2X + 6, vous seriez en grande forme. Donc, vous devez modifier le numérateur un peu. Première multiplier par 2 et diviser l'intégrale de 2:

Parce que vous avez multiplié l'ensemble intégrante de 1, aucun changement net a eu lieu. Maintenant, ajoutez 6 et -6 au numérateur:

Vous avez ajouté 0 à l'intégrale, qui n'a pas changé sa valeur. À ce stade, vous pouvez diviser l'intégrale en deux:

À ce stade, vous pouvez utiliser la substitution de variable pour changer la première intégrale comme suit:

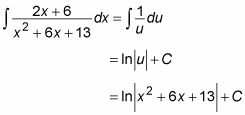
Pour résoudre le deuxième intégrale, compléter le carré dans le dénominateur: Diviser le b terme (6) par 2 et carré, puis représentent la C terme (13) comme étant la somme de ce et tout est laissé:

Maintenant diviser le dénominateur en deux carrés:

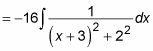
Pour l'évaluer, la formule de l'utilisation intégrante montré dans la section précédente:

Alors, voici la réponse finale pour la seconde intégrale:

Par conséquent, reconstituer la réponse complète comme suit: