Appliquer les théorèmes transversaux
Lorsque vous traversez deux lignes avec une troisième ligne, la troisième ligne est appelé transversal. Vous pouvez utiliser les théorèmes transversales de prouver que les angles sont congruents ou supplémentaire.
Voici un problème qui vous permet de jeter un oeil à quelques-uns des théorèmes en action: Étant donné que les lignes m et n sont parallèles, trouver le mesure de l'angle 1.
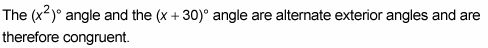
Voici la solution:
(Ou vous pouvez aussi dire que parce que vous avez les parallèles lignes-PLUS-diagramme transversal et deux angles à la fois aiguë de toute évidence, ils doivent être en harmonie.) Mettez-les égaux entre eux et à résoudre pour X:
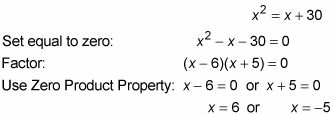
Cette équation a deux solutions, afin de prendre les un à la fois et de les brancher sur les x dans les angles alternes externes.
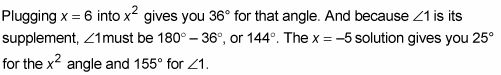
Donc 144 # 176- et 155 # 176- sont vos réponses possibles pour l'angle 1.
Lorsque vous obtenez deux solutions (comme X = 6 et X = -5) À un problème comme celui-ci, vous ne branchez un d'entre eux dans l'une des X's
et l'autre solution dans l'autre X (comme -5 + 30 = 25). Vous devez brancher une des solutions en tous X's, vous donnant un résultat pour les deux angles
alors vous devez brancher séparément l'autre solution dans tous les X's, vous donnant un second résultat pour les deux angles
Angles et les segments ne peuvent pas avoir des mesures négatives ou des longueurs. Assurez-vous que chaque solution pour X produit positif réponses pour tous les angles ou de segments dans un problème.
Si une solution rend tout angle ou un segment dans le diagramme négative, elle doit être rejetée, même si les angles ou de segments que vous vous souciez finissent par être positif. cependant, ne pas rejeter une solution juste parce que X est négative: X peut être négatif pour autant que les angles et les segments sont positifs (X = -5, Par exemple, fonctionne très bien dans ce problème).
Maintenant, voici une preuve qui utilise certains des théorèmes transversales:
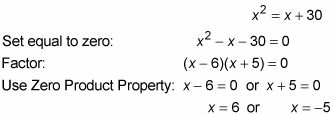
Consultez la preuve formelle:
Déclaration 1:
Motif de la déclaration 1: Compte tenu.
Déclaration 2:
Motif de la déclaration 2: Compte tenu.
Déclaration 3:
Motif de la déclaration 3: Si les lignes sont parallèles, angles intérieurs puis suppléants sont congruents.
Déclaration 4:
Motif de la déclaration 4: Compte tenu.
Déclaration 5:
Motif de la déclaration 5: Si un segment (segment GJ) est soustraite de deux segments congruents, alors les différences sont congruents.
Déclaration 6:
Motif de la déclaration 6: SAS (en utilisant les lignes 1, 3 et 5).
Déclaration 7:
Motif de la déclaration 7: CPCTC (parties correspondantes de congruentes triangles sont congruents).
Déclaration 8:
Motif de la déclaration 8: Si angles alternes sont congruents, alors les lignes sont parallèles.
Étendre les lignes à problèmes transversaux. Extension des lignes parallèles et transversales peut vous aider à voir la façon dont les angles sont liés.
Par exemple, si vous avez du mal à voir ce que l'angle K et l'angle H angles intérieurs sont en effet de substitution (pour l'étape 3 de la preuve),
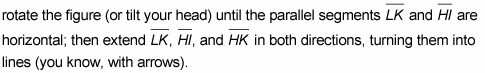
Après avoir fait cela, vous êtes à la recherche au système parallèle en ligne familière montré dans la figure suivante.
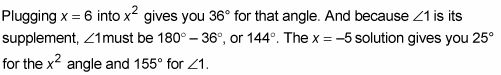
Vous pouvez faire la même chose pour l'angle LJK et l'angle IGH en étendant
Comment prouver triangles semblables avec sas ~ Vous pouvez prouver que les triangles sont semblables en utilisant la méthode SAS ~ (Side-Angle-Side). SAS ~ stipule que si les deux côtés d'un triangle sont proportionnelles à deux côtés d'un autre triangle et les angles inclus sont…
Comment prouver triangles semblables en utilisant le théorème de AA Vous pouvez utiliser la méthode AA (Angle-Angle) pour prouver que les triangles sont semblables. Le théorème de AA stipule que si deux angles d'un triangle sont congruents à deux angles d'un autre triangle, puis les triangles sont semblables.…
Comment prouver qu'un quadrilatère est un rectangle Il ya trois façons de prouver qu'un quadrilatère est un rectangle. Notez que les deuxième et troisième méthodes exigent que vous premier spectacle (ou être donnée) que le quadrilatère en question est un parallélogramme:Si tous les angles…
Comment prouver triangles semblables avec sss ~ Vous pouvez prouver que les triangles sont semblables en utilisant la méthode SSS ~ (Side-Side-Side). SSS ~ stipule que si les rapports des trois paires de côtés de deux triangles correspondant sont égaux, alors les triangles sont semblables.La…
Comment prouver qu'un quadrilatère est un losange Vous pouvez utiliser les six méthodes suivantes pour prouver qu'un quadrilatère est un losange. Les trois dernières méthodes dans cette liste exigent que vous premier spectacle (ou être donnée) que le quadrilatère en question est un…
Comment utiliser castc après avoir prouvé triangles semblables CASTC est tout simplement un acronyme qui signifie «angles correspondants des triangles semblables sont congruents. Vous utilisez souvent CASTC dans une démonstration immédiatement après prouver triangles semblables (exactement de la même…
Stratégies preuve dans la géométrie Savoir comment écrire deux colonnes preuves de géométrie fournit une base solide pour travailler avec des théorèmes. La pratique de ces stratégies vous aidera à rédiger des preuves de géométrie facilement en peu de temps:Faire un plan de…
Preuve stratégies résumées Les stratégies suivantes peuvent vous aider beaucoup quand vous travaillez sur deux colonnes preuves de géométrie. Vous devriez examiner ces stratégies et de pratiquer les utiliser jusqu'à ce qu'ils deviennent intériorisée. Ces stratégies…
Proving angles verticaux sont congruents Lorsque deux lignes se croisent pour effectuer un X, les angles sur les côtés opposés de la X sont appelés angles verticaux. Ces angles sont égaux, et voici le théorème officielle que vous le dit.Les angles verticaux sont congruents: Si deux…
Six théorèmes relatifs au cercle importants Les six théorèmes de cercle est question ici sont tous à quelques variations sur une idée de base sur l'interdépendance des arcs, angles au centre, et les accords (tous les six sont illustrés dans la figure ci-dessous):Les angles et les arcs…
Les composants d'une preuve A deux colonnes géométrie preuve est un problème impliquant un diagramme géométrique de quelque sorte. On vous dit un ou plusieurs choses qui sont vraies sur le schéma (le Givens), Et vous êtes invité à prouver que quelque chose est vrai…
Travailler avec des définitions, des théorèmes, et postulats Définitions, théorèmes et postulats sont les blocs de construction de preuves de géométrie. À quelques exceptions près, tout à fait justifié dans la colonne de raison est l'une de ces trois choses. La figure ci-dessous montre un exemple…
Travailler avec plus d'une transversale Lorsqu'un dessin parallèles lignes-avec-transversal contient plus de trois lignes, l'identification des angles congrus et supplémentaires peut être une sorte de défi. La figure suivante montre deux lignes parallèles avec deux transversales.Si…
Savoir comment les angles, les lignes transversales et concernent UN transversal est une ligne qui coupe au moins deux autres lignes à un moment différent pour chacun. Cette situation implique de multiples angles et les relations d'angle.La transversale dans le diagramme est la ligne qui va vers le bas et vers…