Comment trouver les probabilités pour un échantillon moyen
Dans les statistiques, vous pouvez facilement trouver les probabilités pour une moyenne de l'échantillon si elle a une distribution normale. Même si elle n'a pas une distribution normale, ou la distribution est pas connue, vous pouvez trouver des probabilités si la taille de l'échantillon, n, est assez grand.
La distribution normale est une distribution très conviviale qui dispose d'une table pour trouver des probabilités et tout ce dont vous avez besoin. Par exemple, vous pouvez trouver des probabilités pour
par conversion du
à un z-La valeur et la probabilité de trouver l'aide Z-tableau (voir ci-dessous).
La formule de conversion générale de
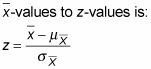
En substituant les valeurs appropriées de la moyenne et erreur standard de
la formule de conversion devient:
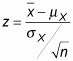
Ne pas oublier de diviser par la racine carrée de n dans le dénominateur de z. Toujours diviser par la racine carrée de n lorsque la question se réfère à la moyenne du X-des valeurs.
Par exemple, supposons X est le temps nécessaire à un employé de bureau choisi au hasard dans un bureau pour taper et envoyer une lettre type de recommandation. Supposer X a une distribution normale, et assume la moyenne est de 10,5 minutes et l'écart-type de 3 minutes. Vous prenez un échantillon aléatoire de 50 employés de bureau et de mesurer leur temps. Quelle est la probabilité que leur durée moyenne est inférieure à 9,5 minutes?
Cette question traduit conclusion
Comme X a une distribution normale pour commencer, vous savez
a aussi une (non approximative) distribution normale exacte. Conversion à z, vous obtenez:
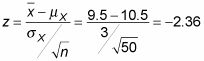
Donc, vous voulez P (Z lt; -2.36).
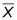
Utilisation de ce qui précède Z-table, vous trouvez que P (Z lt; -2.36) = 0,0091. Donc, la probabilité qu'un échantillon aléatoire de 50 employés de bureau moyenne moins de 9,5 minutes pour remplir cette tâche est de 0,91% (très faible).
Comment trouvez-vous les probabilités pour
si X est pas normal, ou inconnu? À la suite de l'théorème central limite (CLT), la distribution de X peut être non-normale ou même inconnu et aussi longtemps que n est assez grand, vous pouvez toujours trouver approximatif probabilités pour
en utilisant la normale standard (Z-) la distribution et le procédé décrit ci-dessus. Qui est, de convertir à un z-valoriser et trouver des probabilités approximatives en utilisant le Z-table.
Lorsque vous utilisez la CLT pour trouver une probabilité pour
(autrement dit, lorsque la distribution de X est pas normal ou est inconnue), assurez-vous de dire que votre réponse est un approximation. Vous voulez aussi de dire la réponse approximative doit être proche parce que vous avez assez d'une grande n d'utiliser la CLT. (Si n est pas assez grand pour le CLT, vous pouvez utiliser la t-la distribution dans de nombreux cas).
-
Econométrie et la distribution de t -
Mettre les variables sur la même échelle: distribution normale standard (z) -
Statistiques des entreprises: les rendements des actifs modélisation avec une distribution normale -
La différence entre les distributions de probabilités discrètes et continues - Distributions de probabilités discrètes et continues
-
Trouver les valeurs critiques bilatéral pour tester une hypothèse pour un large échantillon
Comment une distribution normale affecte la forme d'une distribution d'échantillonnage Dans les statistiques, lorsque la distribution originale pour une population X est normal, alors vous pouvez aussi supposer que la forme de la distribution d'échantillonnage, ousera également normal, quelle que soit la taille de l'échantillon…
Comment une distribution d'échantillonnage est affectée lorsque la distribution est pas normal Dans les statistiques, si une population X a toute distribution qui est pas normale, ou si sa distribution est inconnu, vous ne pouvez pas dire automatiquement la distribution des moyennes d'échantillona une distribution normale. Mais…
Comment le théorème central limite est utilisée dans les statistiques La distribution normale est utilisée pour aider à mesurer la précision de nombreuses statistiques, dont la moyenne d'échantillon, en utilisant un résultat important appelé le Théorème central limite. Ce théorème vous donne la possibilité…
Comment convertir une distribution d'échantillonnage à une variable aléatoire normale standard utilisant le théorème central limite Vous pouvez utiliser le théorème central limite pour convertir une distribution d'échantillonnage à une variable aléatoire normale standard. Basé sur le théorème central limite, si vous dessinez des échantillons à partir d'une population…
Comment trouver percentiles pour une distribution de t Lorsque vous voulez trouver percentiles pour une t-distribution, vous pouvez utiliser la t-table. UN percentile est un numéro sur une distribution statistique dont le moins que la probabilité est la percentage- donnée par exemple, le 95e centile…
Comment trouver probabilités pour z avec le z-tableau Vous pouvez utiliser le Z-table pour trouver un ensemble complet de probabilités «moins-que" pour une large gamme de z-des valeurs. Pour utiliser le Z-table pour trouver les probabilités pour un échantillon statistique avec une normale…
Comment trouver l'approximation normale de la distribution binomiale avec un large échantillon n Si vous travaillez à partir d'un large échantillon statistique, puis résoudre les problèmes à l'aide de la distribution binomiale peut sembler intimidante. Cependant, il ya en fait un moyen très facile de se rapprocher de la distribution…
Comment trouver la distribution d'échantillonnage d'une proportion d'échantillon Si vous utilisez une taille suffisante de l'échantillon statistique, vous pouvez appliquer le théorème central limite (CLT) à une proportion de l'échantillon pour les données catégorielles pour trouver sa distribution d'échantillonnage. La…
Comment trouver T * -values pour des intervalles de confiance Les intervalles de confiance estimer les paramètres de la population, comme la moyenne de population, en utilisant une statistique (par exemple, la moyenne de l'échantillon) plus ou moins une marge d'erreur. Pour calculer la marge d'erreur pour un…
Comment représenter graphiquement la distribution binomiale Une façon d'illustrer la distribution binomiale est avec un histogramme. Un histogramme montre les valeurs possibles d'une distribution de probabilité d'une série de barres verticales. La hauteur de chaque barre reflète la probabilité de chaque…
Comment dire à un z-distribution à partir d'une distribution de t Bien que la normale (Z-) Distribution et t-la distribution sont similaires, ils regardent différents les uns des autres et sont utilisées à des fins statistiques différentes. La distribution normale est que la distribution en forme de cloche…
Comment les valeurs z sont utilisés dans les statistiques Si un ensemble de données statistiques a une distribution normale, il est coutumier de normaliser toutes les données pour obtenir des scores classiques connues comme z-valeurs ou z-scores. La distribution de z-valeurs prend une distribution…
Distributions statistiques: binomiale, et t-distribution normale Une distribution statistique est une liste des valeurs possibles d'une variable (ou intervalles de valeurs), et combien de fois (ou à ce que la densité) ils se produisent. Il peut prendre plusieurs formes, y compris binomiale, normale, et…
Distributions de probabilité continue Lorsque vous travaillez avec des distributions de probabilités continues, les fonctions peuvent prendre de nombreuses formes. Ceux-ci comprennent uniforme continue, exponentielle, normale, normale standard (Z), approximation binomiale, Poisson…