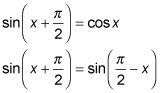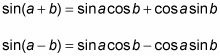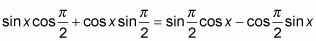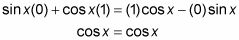En comparant cosinus et sinus fonctions dans un graphique
La relation entre le cosinus et sinus graphiques est que le cosinus est le même que le sinus - seulement il est décalée vers la gauche de 90 degrés, ou PI/ 2. L'équation de la trigonométrie qui représente cette relation est
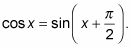
Regardez les graphiques des fonctions sinus et cosinus sur la même axes de coordonnées, comme le montre la figure suivante. Le graphique du cosinus est la note plus sombre Curve façon dont il est décalé vers la gauche de la courbe sinusoïdale.
Les graphiques des fonctions sinus et cosinus illustrent une propriété qui existe depuis plusieurs appariements des différentes fonctions trigonométriques. La propriété représenté ici est basée sur le triangle rectangle et les deux angles aigus ou complémentaires dans un triangle. Les identités qui se posent du triangle sont appelés cofonction identités.
Les identités de cofonction sont les suivantes:
Ces identités montrent comment les valeurs de la fonction des angles complémentaires dans un triangle rectangle sont liés. Par exemple, costheta- = sin (90 # 176- - thêta-) signifie que si thêta- est égal à 25 degrés, alors cos 25 # 176- = sin (90 # 176- - 25 # 176-) = sin 65 # 176-. Cette équation est une façon détournée d'expliquer pourquoi les graphiques des sinus et cosinus sont différentes que par une diapositive. Vous avez probablement remarqué que ces identités Cofonction utilisent toute la différence d'angles, mais la lame de la fonction sinus à la gauche était une somme. Le graphique sine décalé et le graphique de cosinus sont vraiment équivalent - ils deviennent des graphiques de la même série de points. Voici comment faire pour prouver cette affirmation.
Vous voulez montrer que la fonction sinus, a glissé de 90 degrés vers la gauche, est égal à la fonction cosinus:
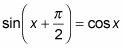
Remplacer cos X avec son identité de cofonction.
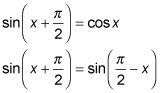
Appliquer les deux identités pour le sinus de la somme et la différence des deux angles.
Les deux identités sont
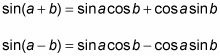
En substituant dans la Xs 'et les angles,
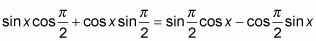
Simplifier les termes en utilisant les valeurs des fonctions.
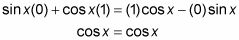
Donc, vous voyez, le graphique sine décalé est égal à la courbe de cosinus.
-
En appliquant les formules somme et de différence pour les cosinus pour trouver le cosinus de la somme ou la différence de deux angles -
Comment représenter graphiquement sinus, cosinus et tangente -
Comment simplifier une expression en utilisant même des identités / impairs -
Comment simplifier une expression en utilisant des identités réciproques -
Intégrer lorsque les pouvoirs de sinus, cosinus sont encore, non négatif -
Domaine et des fonctions sinus et cosinus
Sine express en termes de cosinus Même si chaque fonction de la trigonométrie est parfaitement merveilleux, être en mesure d'exprimer chaque fonction trig en termes de l'un des cinq autres fonctions trigonométriques est souvent à votre avantage. Par exemple, vous pouvez avoir…
Sine express en termes de tangente Même si chaque fonction de la trigonométrie est parfaitement merveilleux, être en mesure d'exprimer chaque fonction trig en termes de l'un des cinq autres fonctions trigonométriques est souvent à votre avantage. Par exemple, vous pouvez avoir…
Trouver opposé angle identités trigonométriques La identités angle opposé changer fonctions trigonométriques d'angles négatifs aux fonctions d'angles positifs. Angles négatifs sont parfaits pour décrire une situation, mais ils ne sont pas vraiment à portée de main quand il vient à les…
Trouver ratio de la trigonométrie identités Trig a deux identités appelés rapport identités. Cette étiquette peut être source de confusion, parce que toutes les fonctions trigonométriques sont définis par les ratios. Quelque part le long de la ligne, cependant, les mathématiciens…
Graphiquement une fonction sinusoïdale utilisant une amplitude La fonction sinus et une de ses variations ont deux caractéristiques importantes: l'amplitude et la période de la courbe. Vous pouvez déterminer ces caractéristiques en regardant soit le graphe de la fonction ou de son équation.La amplitude de…
Graphique fonctions sinus et cosinus inverse Les graphiques des fonctions trigonométriques inverses sont relativement unique- par exemple, sinus inverse et le cosinus inverse sont plutôt abrupte et décousue. Ces graphiques sont importants en raison de leur impact visuel. Surtout dans le…
Comment reconnaître graphiques trigonométriques de base Les graphiques des fonctions trigonométriques ont beaucoup de similitudes et de différences. Les graphiques du sinus et cosinus se ressemblent beaucoup, tout comme la tangente et cotangente, puis la sécante et cosécante ont des similitudes. Mais…
Comment utiliser l'identité angle somme quand vous ne savez pas l'angle Dans certains problèmes de trigonométrie, vous ne pouvez pas savoir ce que la mesure d'un angle est, mais vous savez quelque chose sur les valeurs de la fonction de l'angle. Par exemple, supposons que vous avez deux angles, alpha dans le second…
Comment utiliser les identités de soustraction dans un problème trig Vous pouvez trouver des valeurs de la fonction d'angles en utilisant des identités angle addition. Et vous avez plus de possibilités pour trouver les valeurs de la fonction d'angles lorsque vous utilisez la soustraction à un problème de trig.…
Produit identités-à-somme Les trigonométriques produit-à-somme identités se ressemblent beaucoup. Vous devez porter une attention particulière aux différences subtiles de sorte que vous pouvez les appliquer correctement. Même si le produit semble agréable et compact,…
Pythagore sinus et cosinus identités sur un cercle unité Si vous avez déjà demandé pourquoi l'identité de Pythagore, le péché2thêta- + cos2thêta- = 1, est si important, et d'où il vient, alors lisez la suite. Cette identité est importante car elle établit une expression impliquant des fonctions…
Sinus et cosinus avec l'algèbre Vous pouvez rapprocher, de façon assez précise, le sinus et cosinus des angles avec un infini série, qui est la somme des termes de certaines séquences, ou une liste, de numéros. Prenez note, cependant, que la série de sinus et cosinus sont…
Identités Sum-à-produit La somme des identités de produits sont utiles pour modéliser ce qui se passe avec des fréquences sonores. Pensez à deux tonalités différentes représentées par des courbes sinusoïdales. Ajoutez-les ensemble, et ils ont battu les uns contre…
La fonction cosinus: adjacente sur l'hypoténuse La fonction trig cosinus, abrégé cos, travaille en formant ce rapport: adjacente / hypoténuse. Dans la figure, vous voyez que les cosinus des deux angles sont comme suit:La situation avec les rapports est la même que pour la fonction sinus - les…