Comment vérifier une convolution problème intégrante numérique

Voici une solution d'analyse détaillée à un problème intégrante de convolution, suivie par la vérification numérique détaillée, en utilisant PyLab du shell interactif IPython (la version QT en particulier). L'intention de la solution numérique est de démontrer comment les outils informatiques peuvent vérifier des solutions analytiques aux problèmes de convolution.

Mettre en place PyLab

Pour commencer à PyLab et le shell interactif IPython, vous pouvez facilement mettre en place les outils sur Mac OS, Windows et Ubuntu Linux.

Mise en place sur Ubuntu Linux est peut-être le plus facile parce que vous pouvez simplement utiliser la Ubuntu Software Center. Sur Mac OS et Windows, vous pouvez utiliser un installation monolithique, qui installe plus tout ce que vous devez à la fois. Découvrez la version gratuite de Enthought, mais d'autres sont disponibles sur le web.

Vérifiez convolution en temps continu

Voici un exemple de convolution utilisant des signaux de mesure finis. Solutions analytiques complètes sont inclus, mais l'accent est mis sur la vérification numérique, en particulier, en utilisant PyLab et le module de code personnalisé disponible gratuitement ssd.py mentionné précédemment.

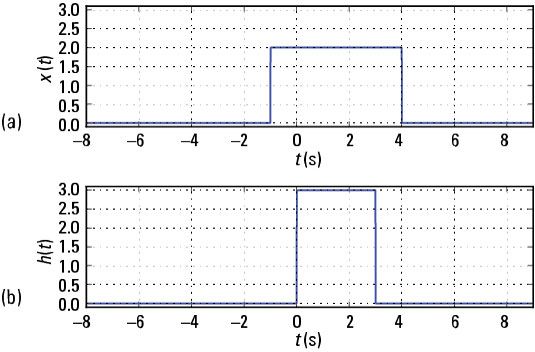
Considérons l'intégrale de convolution pour deux signaux en temps continu X(t) Et h(t) Indiqué.

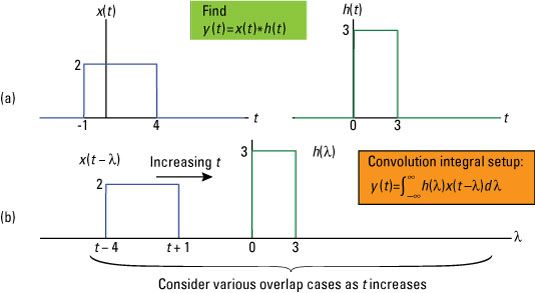
Pour en arriver à la solution analytique, vous devez découper le problème en cinq cas, ou des intervalles de temps t où vous pouvez évaluer l'intégrale pour former une solution contiguë morceaux. Lorsque vous mettez ces cinq intervalles contigus ensemble, vous avez une solution complète pour toutes les valeurs de t:

De l'étude des intégrales de convolution, vous découvrez que vous pouvez écrire le soutien ou l'intervalle actif pour la sortie y(t) En fonction des intervalles de support pour chacun des signaux d'entrée. Ce résultat indique que l'intervalle de support de sortie va de la somme des valeurs de départ pour X(t) Et h(t) Et se termine à des valeurs de fin. Ainsi, l'intervalle de support pour y(t) Est au plus

Dans cet exemple, chaque cas est à traiter comme une étape dans la solution qui suit:

• Cas 1: Vous commencez avec t + 1 lt; 0, ou de manière équivalente t lt; -1. Le produit de formes d'onde h(# 955-) Et X(t - # 955-) ne se chevauchent pas dans la convolution intégrand intégrante, donc pour le cas 1 l'intégrale est juste y(t) = 0 pour t lt; -1.

• 
  
  
  
  

  Cas 2: Considérons l'intervalle suivant à droite de cas 1. Cette affaire est formé par la condition commune du bord de signal à t + 1 # 8805- 0 et t + 1 lt; 3, ce qui correspond à l'écriture -1 # 8804- t lt; 2. L'intégrant de l'intégrale de convolution est de 2 x 3 avec les limites d'intégration allant de 0 à t + 1.

  Tu trouves y(t) Dans cet intervalle par l'évaluation de l'intégrale de convolution:

  

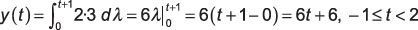
• Case 3: Le prochain intervalle de la série est t + 1 # 8805- 3 ​​et t - 4 lt; 0 ou 2 # 8804- t lt; 4. Le intégrant est à nouveau 2 x 3, mais maintenant les limites d'intégration fonctionne de 0 à 3. Évaluer les rendements intégrales de convolution qui suit:

  

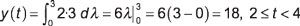
• Case 4: L'intervalle final impliquant un chevauchement de signal se produit lorsque t - 4 # 8805- 0 et t - 4 lt; 3, ce qui implique que quatre # 8804- t # 8804- 7. Les limites d'intégration exécutés à partir t - 4-3, de sorte que le résultat de convolution intégrale est

  

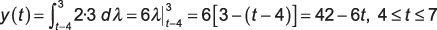
• Case 5: Vous pouvez voir que lorsque t - 4> 3 ou t > 7, aucun chevauchement se produit entre les signaux de l'intégrale, de sorte que la sortie est y(t) = 0, t > 7.

Collecte les différents morceaux de la solution, vous avez la suivante:

Vérification de cette solution avec Python comporte deux étapes: (1) traçant la solution analytique et (2) le comparant avec l'intrigue de la solution numérique, en utilisant les fonctions trouvés dans le module de code ssd.py. Voici les détails pour remplir ces étapes:

1. Créer une fonction par morceaux en Python que vous pouvez ensuite évaluer sur une plage de valeurs de temps défini par l'utilisateur.

   Vous pouvez écrire cette fonction droite dans la coquille IPython comme montré ici:

   Dans [68]: Def pulse_conv (t): ...: Y = zéros (len (t)) # initialiser tableau de sortie ...: pour k, tk dans enumerate (t): # make Y (t) des valeurs ...: Si les savoirs traditionnels> = -1 et tk lt; 2: ...: y [k] = 6 * tk + 6 ...: Elif tk> = 2 et tk lt; 4: ...: y [k] = 18 ...: Elif tk> = 4 et tk lt; = 7: ...: y [k] = 42-6 * tk ...: retour Y

   Notez que le langage Python est sensible à tirets, donc attention aux tirets lorsque vous entrez ce code dans IPython. Les bonnes nouvelles sont que IPython comprend les besoins de Python et fait un bon travail de l'indentation bloc de code automatiquement.

2. Évaluer numériquement la convolution en créant d'abord des représentations des formes d'onde réelles de la convolution et en effectuant ensuite la convolution numérique.

   Pour avoir accès aux fonctions dans le module ssd.py, vous devez importer le module dans votre session IPython, en utilisant Dans [69]: l'importation ssd.

   Ensuite, vous pouvez accéder aux fonctions du module en utilisant le namespace prefix ssd. La fonction y, ny = ssd.conv_integral (x1, TX1, x2, TX2, l'étendue = ('f', 'f')) effectue la convolution réelle.

   Vous chargez versions de temps échantillonnée des signaux à convolution dans les arguments x1 et x2, avec TX1 et TX2 étant les axes de temps correspondantes. Tous les quatre de ces variables sont NumPy ndarrays. La fonction retourne le résultat de convolution y suivi par New York, comme un tuple Python. Les formes d'impulsion rectangulaires sont créées en utilisant la fonction ssd.rect (n, tau) et l'axe de décalage dans le temps dans les arguments de la fonction.

   Mettre le tout ensemble, le code pour la sortie numérique rapprochant intégrante de convolution est la suivante (seules les déclarations de code critiques représentés):

   Dans [89]: T = arange (-8,9, 0,01) Dans [90]: Xc1 = 2 * ssd.rect (t-1.5,5) Dans [91]: Hc1 = 3 * ssd.rect (t-1.5,3) Dans [93]: Intrigue secondaire (211) Dans [94]: Parcelle (t, xc1) Dans [99]: Intrigue secondaire (212) Dans [100]: Parcelle (t, HC1) Dans [101]: Savefig ('c1_intputs.pdf') Dans [115]: Yc1_num, tyc1 = ssd.conv_integral (xc1, t, HC1, t) le soutien de sortie: (-16.00, 17,98) Dans [116]: Intrigue secondaire (211) Dans [117]: Parcelle (t, pulse_conv (t)) Dans [123]: Intrigue secondaire (212) Dans [125]: Parcelle (tyc1, yc1_num) Dans [130]: Savefig ('c1_outputs.pdf')

   La figure suivante montre les parcelles des signaux X(t) Et h(t).

   

Enfin, la représentation numérique de y(t) Est tracé en même temps que la solution analytique indiqué.

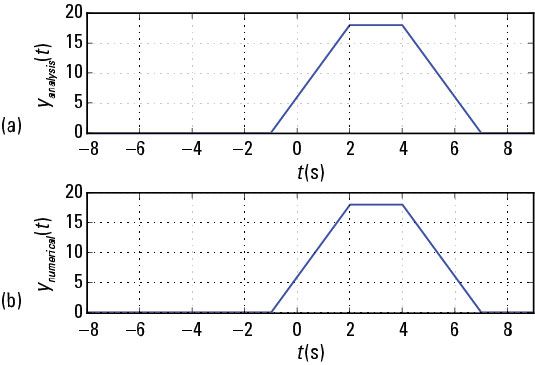
Du point de vue de la parcelle, les deux solutions sont d'accord, de sorte que la solution analytique est confirmée.