Comment faire pour résoudre les systèmes linéaires qui ont plus de deux équations

Lorsque votre pré-calcul instructeur vous demande de résoudre plus grands systèmes d'équations linéaires, ces équations impliqueront plus de deux équations qui vont de pair avec plus de deux variables. Vous pouvez écrire ces grands systèmes dans le formulaire AX + By + Cz + . . . = K où tous les coefficients (K) et sont des constantes. Ces systèmes linéaires peuvent avoir de nombreuses variables, et vous pouvez résoudre ces systèmes aussi longtemps que vous avez une équation unique par variable. En d'autres termes, trois variables ont besoin de trois équations pour trouver une solution unique, quatre variables besoin de quatre équations, et dix variables devrait avoir dix équations, et ainsi de suite.

Pour ces types de systèmes non linéaires, les solutions que vous pouvez trouver varient considérablement:

• Vous trouverez peut-être pas de solution.

• Vous pouvez trouver un solution unique.

• Vous pouvez avoir une infinité de solutions.

Le nombre de solutions que vous trouvez dépend de comment les équations interagissent les uns avec les autres. Parce que les systèmes linéaires d'équations décrivent trois variables d'avions, et non pas en tant que lignes (équations à deux variables ne), la solution du système dépend de la façon dont les plans se trouvent dans l'espace tridimensionnel par rapport à l'autre. Malheureusement, tout comme dans les systèmes d'équations à deux variables, vous ne pouvez pas dire combien de solutions système a sans faire le problème. Traitez chaque problème que si elle dispose d'une solution, et si elle ne le fait pas, vous aurez soit arriver à une déclaration qui est jamais vrai (pas de solutions) ou est toujours vrai (ce qui signifie que le système a une infinité de solutions).

En règle générale, vous devez utiliser la méthode d'élimination plus d'une fois pour résoudre des systèmes avec plus de deux variables et deux équations.

Par exemple, supposons un problème vous demande de résoudre le système suivant:

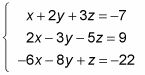
Pour trouver la solution (s), suivez ces étapes:

1. Regardez les coefficients de toutes les variables et de décider quelle variable est plus facile à éliminer.

   
   
   
   
   

   Avec l'élimination, vous voulez trouver le plus petit commun multiple (LCM) pour les coefficients de l'une des variables, donc aller avec celui qui est le plus facile. Dans ce cas, vous devez éliminer le X-variable.

2. Mis à part deux des équations et d'éliminer une variable.

   En regardant les deux premières équations, vous devez multiplier le haut par -2 et l'ajouter à la deuxième équation. Ce faisant, vous obtenez l'équation suivante:

   

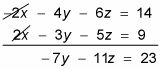
3. Mis à part deux autres équations et d'éliminer la même variable.

   Le premier et le troisième équations permettent d'éliminer facilement X de nouveau. Multiplier l'équation haut par 6 et l'ajouter à la troisième équation pour obtenir l'équation suivante:

   

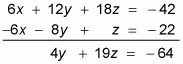
4. Répétez le processus d'élimination avec vos deux nouvelles équations.

   Vous avez maintenant ces deux équations à deux variables:

   

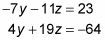
   Vous devez éliminer une de ces variables. Cet exemple élimine le y-en multipliant la variable de l'équation haut et par le fond 4 par 7 et en ajoutant ensuite les équations. Voici ce que cette étape vous donne:

   

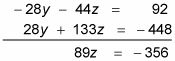
5. Résoudre l'équation finale pour la variable qui reste.

   Si 89z = -356, Puis z = -4.

6. Remplacer la valeur de la variable résolu dans l'une des équations qui a deux variables pour résoudre pour une autre.

   Cet exemple utilise l'équation -7y - 11z = 23. En substituant, vous avez -7y - 11 (-4) = 23, ce qui simplifie à -7y + 44 = 23. Maintenant, finir le travail: -7y = -21, y = 3.

7. Remplacez les deux valeurs que vous avez maintenant dans l'une des équations originales à résoudre pour la dernière variable.

   Cet exemple utilise la première équation dans le système d'origine, qui devient maintenant X + 2 (3) + 3 (-4) = -7. Simplifier pour obtenir votre réponse finale:

1. X + 6 - 12 = -7

2. X - 6 = -7

3. X = -1

Les solutions à cette équation sont X = -1, y = 3, et z = -4.

Ce processus est appelé la substitution de retour parce que vous résoudre littéralement pour une variable puis de travailler votre chemin vers l'arrière à résoudre pour les autres. Dans ce dernier exemple, vous êtes passé de la solution pour une variable dans une équation à deux variables dans les deux équations à la dernière étape avec trois variables dans trois équations. Toujours déplacer à partir de la plus simple à la plus compliquée.