Comment utiliser les limites pour déterminer la continuité

Ici, vous prenez connaissance de continuité pour un peu, puis passer à la connexion entre la continuité et les limites, et enfin passer à la définition formelle de la continuité.

Définition de bon sens de la continuité

La continuité est un tel concept simple - vraiment. UN continu fonction est simplement une fonction sans lacunes - une fonction que vous pouvez dessiner sans prendre votre crayon le papier. Considérons les quatre fonctions dans ce chiffre.

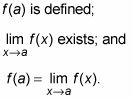
Que ce soit ou non une fonction est continue est presque toujours évident. Les deux premières fonctions dans ce chiffre - F (X) Et g(X) - N'a pas de lacunes, ils sont donc continue. Les deux suivantes - p(X) Et q(X) - Ont des lacunes au X = 3, donc ils ne sont pas en continu.

Voilà tout ce qui est à lui! Eh bien, pas tout à fait. Les deux fonctions avec écarts ne sont pas continue partout, mais parce que vous pouvez dessiner sections d'entre eux sans prendre votre crayon le papier, vous pouvez dire que des parties de ces fonctions sont continues.

Et parfois, une fonction est continue partout où il est défini. Une telle fonction est décrite comme étant continue sur toute son domaine, ce qui signifie que son ou des espaces se produisent à X-des valeurs où la fonction est indéfini. La fonction p(X) Est continu sur toute sa domain- q(X), D'autre part, est non continu sur la totalité de son domaine, car il est à pas continu X = 3, qui est dans le domaine de la fonction. Souvent, la question importante est de savoir si une fonction est continue à un particulier X-valeur. Il est à moins qu'il y est une lacune.

Toutes les fonctions polynômes sont continues partout. Toutes les fonctions rationnelles - une fonction rationnelle est le quotient de deux fonctions polynômes - sont continues sur l'ensemble de leurs domaines.

La connexion continuité limite

Avec une grande exception (que vous aurez dans un instant), la continuité et les limites vont de pair. Par exemple, examiner à nouveau les fonctions F, g, p, et q. Fonctions F et g sont continues au X = 3, et ils ont tous les deux limites à X = 3. Fonctions p et q, d'autre part, ne sont pas en continu X = 3, et ils ne sont pas des limites à X = 3. L'exception à la règle concerne les fonctions avec des trous. En fait, quand vous venez au fond des choses, l'exception est plus important que la règle. Considérons les deux fonctions dans la figure suivante.

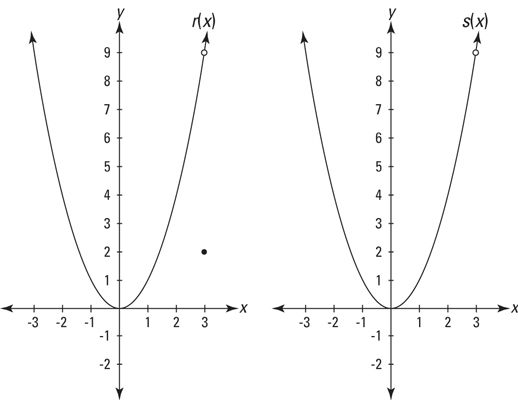
Ces fonctions ont des lacunes au X = 3 et ne sont évidemment pas en continu, mais ils ont des limites que X approches 3. Dans chaque cas, la limite est égale à la hauteur du trou. Un trou infinitésimale dans une fonction est le seul endroit Une fonction peut avoir une limite où il est pas continue.

Les deux fonctions de l'illustration ont la même limite que X 3- approche de la limite est de 9, et les faits qui r(3) = 2, et que s(3) est indéfini ne sont pas pertinents. Pour les deux fonctions, comme X zéros dans le 3 de chaque côté, la hauteur de la fonction zéros sur la hauteur du trou - qui est la limite.

La limite à un trou est la hauteur d'un trou.

Définition formelle de la continuité

Une fonction F (X) Est continue en un point X = un si les trois conditions suivantes sont remplies:

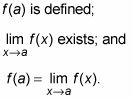
Tout comme avec la définition formelle d'une limite, la définition de la continuité est toujours présentée comme un test en 3 parties, mais la condition 3 est le seul que vous devez vous préoccuper, car 1 et 2 sont construits en 3. Vous devez vous rappeler, cependant , cette condition est 3 pas satisfait lorsque les côtés gauche et droit de l'équation sont tous les deux non défini ou inexistante.