Comment intégrer les compositions de fonctions
Compositions contenant des fonctions - qui est, une fonction imbriquée dans une autre - sont de la forme F(g(X)). Vous pouvez les intégrer en substituant u = g(X) quand
Vous savez comment intégrer la fonction externe F.
La fonction interne g(X) différencie à une constante - qui est, il est de la forme hache ou hache + b.
Voici un exemple. Supposons que vous souhaitez intégrer la fonction, csc2 (4X + 1).
Ceci est une composition de deux fonctions:
La fonction externe F est le csc2 (uFonction).
La fonction interne est g(X) = 4X + 1, ce qui le différencie de la constante 4.
La composition est maintenue par l'égalité u = 4X + 1. Autrement dit, les deux fonctions de base F(u) = Csc2 u et g(X) = 4X + 1 sont constitués par l'égalité u = 4X + 1 pour produire la fonction F(g(X)) = Csc2 (4X + 1).
Les deux critères sont respectés, cette intégrale est un candidat de choix pour la substitution à l'aide u = 4X + 1. Voilà comment vous le faites:
Déclarez une variable u et la remplacer dans l'intégrale:
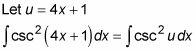
Différencier u = 4X + 1 et d'isoler le X terme.
Cela vous donne l'écart, du = 4dx.
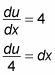
Suppléant du/ 4 pour dx dans l'intégrale:
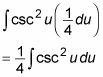
Évaluer l'intégrale:
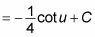
Substituer retour 4X + 1 pour u:
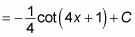
Voici un exemple de plus. Supposons que vous voulez évaluer l'intégrale suivante:
Ceci est une composition de deux fonctions:
La fonction externe F est une fraction - techniquement, un exposant de -1 - que vous savez comment intégrer.
La fonction interne est g(X) = X - 3, qui se différencie à 1.
La composition est maintenue par l'égalité u = X - 3. Autrement dit, les deux fonctions de base
sont constitués par l'égalité u = X - 3 pour produire la fonction
Les critères sont respectés, de sorte que vous pouvez intégrer à l'aide de l'égalité u = X - 3:
Déclarez une variable u et la remplacer dans l'intégrale:
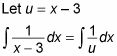
Différencier u = X - 3 et isoler le X terme.
Cela vous donne l'écart = dx du.
Suppléant du pour dx dans l'intégrale:
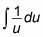
Évaluer l'intégrale:
= Ln |u| + C
Substituer retour X - 3 pour u:
= Ln |X - 3 | + C
Trouver l'intégrale de fonctions imbriquées Parfois, vous avez besoin d'intégrer une fonction qui est la composition de deux fonctions - par exemple, la fonction 2X imbriquée dans une fonction sinusoïdale. Si vous étiez de différenciation, vous pouvez utiliser la règle de la chaîne.…
Comment intégrer une série de puissance Parce que la série de puissance ressemblent polynômes, ils sont simples à intégrer l'aide d'un processus simple en trois étapes qui utilise la règle Somme, Constant règle multiple, et de la règle d'alimentation.Par exemple, jetez un oeil à…
Comment intégrer une fonction multiplié par un ensemble de fonctions imbriquées Parfois vous avez besoin pour intégrer le produit d'une fonction (X) Et une composition de fonctions (par exemple, la fonction 3X2 + 7 imbriqué dans une fonction de la racine carrée). Si vous étiez de différenciation, vous pouvez utiliser une…
Comment intégrer les expressions rationnelles utilisant la somme, multiple constant, et les règles d'alimentation Dans de nombreux cas, vous pouvez démêler expressions rationnelles velues et de les intégrer en utilisant les règles anti-différenciation plus la règle Somme, Constant règle multiple, et de la règle d'alimentation.La règle Somme pour…
Comment intégrer les puissances paires de sinus et cosinus Vous pouvez intégrer des pouvoirs même de sinus et cosinus. Par exemple, si vous vouliez intégrer le péché2 X et cos2 X, vous pouvez utiliser ces identités de deux demi-angle trigonométrie:Voici comment vous intégrez cos2 X:Utilisez…
Comment résoudre intégrales avec la substitution de variable En calcul, vous pouvez utiliser la substitution de variables pour évaluer une intégrale complexe. La substitution de variable vous permet d'intégrer lorsque la règle Somme, Constant règle multiple, et de la règle d'alimentation ne fonctionnent…
Intégrer une fonction en utilisant le cas sécant Lorsque la fonction que vous intégrez comprend un terme de la forme (bx2 - un2)n, attirer votre trig substitution triangle pour le cas sécant. Par exemple, supposons que vous voulez évaluer cette intégrale:Ceci est un cas sécant, car un…
Intégrer une fonction en utilisant le cas sine Lorsque la fonction vous intégrez comprend un terme de la forme (un2 - bx2)n, attirer votre trig substitution triangle pour le cas sine. Par exemple, supposons que vous voulez évaluer l'intégrale suivante:Ceci est une affaire sine, car une…
Intégrer une fonction en utilisant le cas tangent Lorsque la fonction vous intégrez comprend un terme de la forme (un2 + X2)n, attirer votre trigonométrie substitution triangle pour le cas de la tangente. Par exemple, supposons que vous voulez évaluer l'intégrale suivante:Ceci est un cas…
Intégrer pouvoirs de cotangentes et cosécantes Vous pouvez intégrer pouvoirs de cotangentes et cosécantes similaires à la façon dont vous faites tangentes et sécantes. Par exemple, voici comment cot intégrer8 X csc6 X:Décoller un csc2 X et le placer à côté de la dx:Utilisez le + lit…
De mesure de volume sous une surface en utilisant une intégrale double Une intégrale double vous permet de mesurer le volume sous une surface délimitée que par un rectangle. Intégrales définies constituent un moyen fiable pour mesurer la surface signé entre une fonction et la X-axe délimitée par les deux…
Résolvez fonctions composés où la fonction intérieure est la hache Lors du calcul des problèmes de calcul, certaines intégrales de fonctions composés F (g(X)) Sont faciles à faire rapidement. Ceux-ci incluent des fonctions de composés pour lesquels vous savez comment intégrer la fonction externe F, et la…
En substituant les expressions de la forme f (x) multiplié par g (x) Quand g'(X) = F(X), Vous pouvez utiliser la substitution u = g(X) D'intégrer expressions de la forme F(X) multiplié par g(X). La substitution de variable permet de combler les lacunes laissées par l'absence d'une règle de produit et une règle…
En substituant les expressions de la forme f (x) multiplié par h (g (x)) Quand g'(X) = F(X), Vous pouvez utiliser la substitution u = g(X) D'intégrer expressions de la forme F(X) multiplié par h(g(X)), à condition que h est une fonction qui vous savez déjà comment intégrer.La substitution de variable permet de…