Analyser un circuit de premier ordre rc en utilisant des méthodes de Laplace

Utilisation de la transformée de Laplace dans le cadre de votre analyse de circuit vous fournit une prédiction de la réponse du circuit. Analyser les pôles de la transformée de Laplace pour avoir une idée générale du comportement de sortie. Pôles réels, par exemple, indiquent le comportement de sortie exponentielle.

Suivez ces étapes de base pour analyser un circuit en utilisant des techniques de Laplace:

1. Développer l'équation différentielle dans le domaine du temps en utilisant les lois de Kirchhoff et équations d'éléments.

2. Appliquer la transformation de Laplace de l'équation différentielle pour mettre en équation la s-domaine.

3. Résoudre algébriquement pour la solution, ou transformer réponse.

4. Appliquer la transformation de Laplace inverse pour produire la solution de l'équation différentielle originale décrite dans le domaine temporel.

Pour vous familiariser avec ce processus, il vous suffit de pratiquer l'appliquer à différents types de circuits tels que une RC (résistance-condensateur) circuit, un RL (résistance-inductance) circuit, et une (résistance-inductance-condensateur) circuit RLC .

Considérons le circuit RC série de premier ordre simple montré ici. Pour mettre en place l'équation différentielle pour ce circuit de série, vous pouvez utiliser la loi de tension de Kirchhoff (KVL), qui dit la somme de la tension monte et descend autour d'une boucle est égal à zéro. Ce circuit a l'équation suivante KVL autour de la boucle:

-v_S(t) + v_r(t) + v_c(t) = 0

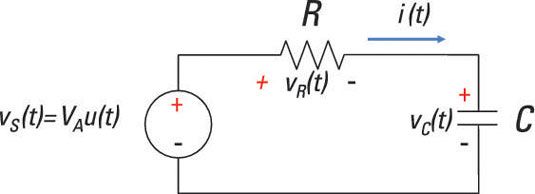
Ensuite, formuler l'équation de l'élément (ou i-v caractéristique) pour chaque appareil. L'équation de l'élément de la source est

v_S(t) = V_UNu (t)

Utiliser la loi d'Ohm pour décrire la tension aux bornes de la résistance:

v_R(t) = i (t) R

Élément de l'équation de la capacité est donnée à titre

En substituant cette expression pour ce) en v_R(t) vous donne l'expression suivante:

En substituant v_R(t), v_C(t), et v_S(t) dans l'équation KVL conduit à

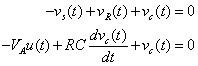
Maintenant réorganiser l'équation pour obtenir l'équation souhaitée différentiel de premier ordre:

Maintenant vous êtes prêt à appliquer la transformation de Laplace de l'équation différentielle dans le s-domaine. Le résultat est

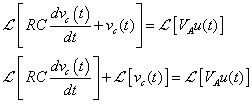
Sur la gauche, la propriété de linéarité a été utilisé pour prendre la transformée de Laplace de chaque terme. Pour le premier terme sur le côté gauche de l'équation, vous utilisez la propriété de différenciation, qui vous donne

Cette équation utilise V_C(s) = # 8466- [v_C(t)], et V₀ est la tension initiale aux bornes du condensateur.

En utilisant le tableau suivant, la transformée de Laplace d'une fonction de l'étape vous fournit avec ceci:

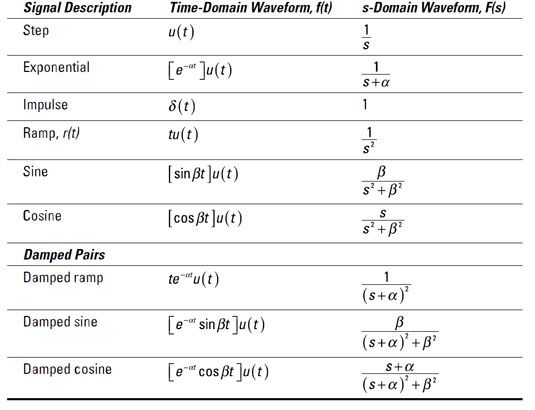
Sur la base des expressions précédentes pour la transformation de Laplace, l'équation différentielle devient le suivant:

Ensuite, réorganiser l'équation:

Résoudre pour la sortie V_c(s) pour obtenir la solution suivante transformer:

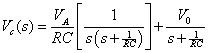
En effectuant une transformée de Laplace inverse de V_C(s) pour un état initial donné, cette équation conduit à la solution v_C(t) de l'équation originale différentiel de premier ordre.

À l'étape 3 du processus. Pour obtenir la solution dans le domaine temporel v_C(t), vous devez faire une expansion de fraction partielle pour le premier terme sur le côté droit de l'équation précédente:

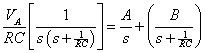
Vous devez déterminer les constantes UN et B. Pour simplifier l'équation précédente, multiplier les deux côtés par s (s + 1 / RC) de se débarrasser des dénominateurs:

Algébriquement réorganiser l'équation en recueillant des termes semblables:

Afin que le côté gauche de l'équation précédente pour être égal à zéro, les coefficients doivent être zéro (A + B = 0 et A - V_UN = 0). Pour les constantes UN et B, vous vous retrouvez avec A = V_UN et B = -V_UN. Remplacez ces valeurs dans l'équation suivante:

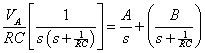
La substitution vous conduit à:

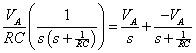
Maintenant substituer l'expression précédente dans le V_C(s) l'équation pour obtenir la solution transformer:

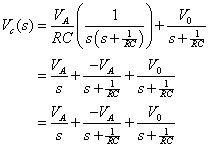
Cela complète l'expansion de fraction partielle. Vous pouvez ensuite utiliser le tableau donné plus tôt pour trouver la transformée de Laplace inverse pour chaque terme sur le côté droit de l'équation précédente.

Le premier terme a la forme d'une fonction de l'étape, et les deux derniers termes ont la forme d'une exponentielle, de sorte que la transformée de Laplace inverse de l'équation précédente vous conduit à la solution suivante v_C(t) dans le domaine temporel:

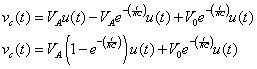
Le résultat montre que le temps t tend vers l'infini, le condensateur se charge à la valeur de l'entrée V_UN. En outre, la tension initiale du condensateur finalement éteint à zéro après une longue période de temps (environ 5 constantes de temps RC),.