Décrire circuits de second ordre avec des équations différentielles du second ordre

Si vous pouvez utiliser une équation différentielle du second ordre pour décrire le circuit que vous cherchez à, alors vous avez affaire à un circuit de deuxième ordre. Circuits comprenant un inducteur, un condensateur, et résistance connectée en série ou en parallèle sont des circuits du second ordre. Voici circuits de second ordre entraînées par une source d'entrée, ou fonction de forçage.

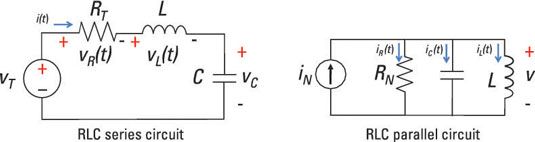
Obtenir une solution unique à une équation différentielle du second ordre, il faut connaître les états initiaux du circuit. Pour un circuit de deuxième ordre, vous devez connaître la tension de condensateur initial et le courant initial de l'inducteur. La connaissance de ces États au moment t = 0 vous fournit une solution unique pour tous les temps après le temps t = 0.

Utilisez ces étapes lors de la résolution d'une équation différentielle du second ordre pour un circuit de deuxième ordre:

1. Trouver la réponse d'entrée zéro par le réglage de la source d'entrée à 0, de sorte que la sortie est uniquement due aux conditions initiales.

2. Trouver la réponse à l'état zéro par le réglage des conditions initiales égal à 0, de sorte que la sortie est due seulement au signal d'entrée.

   Zéro conditions initiales signifie que vous avez 0 initial tension de condensateur et 0 courant initial d'induction.

   La réponse à l'état zéro vous oblige à trouver les solutions homogènes et notamment:
3. 
   
   
   
   

   Solution homogène: Quand il n'y a pas de signal d'entrée ou de forcer la fonction - qui est, quand v_T(t) = 0 ou je_N(t) = 0 - vous avez la solution homogène.

4. Solution particulière: Quand vous avez une entrée différente de zéro, la solution suit la forme du signal d'entrée, vous donnant la solution particulière. Par exemple, si votre entrée est une constante, alors votre solution particulière est également une constante. De même, si vous avez une fonction sinus ou cosinus comme entrée, la sortie est une combinaison de fonctions sinus et cosinus.

5. Ajouter les réponses zéro entrée et étatiques zéro pour obtenir la réponse totale.

   Parce que vous avez affaire à des circuits linéaires, vous souhaitez utiliser la superposition de trouver la réponse totale.

Pour trouver la réponse totale pour une équation différentielle du second ordre à coefficients constants, vous devez d'abord trouver la solution homogène en utilisant une équation caractéristique algébrique et assumer les solutions sont des fonctions exponentielles. Les racines de l'équation caractéristique vous donnent les constantes trouvées dans l'exposant de la fonction exponentielle.

Devinez à une solution élémentaire: La fonction exponentielle naturelle

Ceci est juste une approche pour résoudre les circuits de second ordre. Les bonnes nouvelles sont qu'il convertit un problème impliquant une équation différentielle à celui qui utilise uniquement l'algèbre.

Considérons l'équation différentielle suivante comme un exemple numérique avec fonction de forçage à zéro v_T(t) = 0:

La solution de cette équation différentielle est appelé la solution homogène v (t). Une approche classique consiste à donner à votre meilleur coup à deviner la solution. Essayer v (t) = e^kt. La fonction exponentielle travaille pour une équation du premier ordre, il doit donc travailler pour une équation de second ordre, aussi.

Lorsque vous prenez la dérivée de la exponentielle naturelle e^kt, vous obtenez la même chose, multiplié par une constante k. Vous voyez comment la fonction exponentielle est votre véritable Amigo à résoudre des équations différentielles de ce genre.

De calcul à l'algèbre: l'aide de l'équation caractéristique

Pour résoudre une équation différentielle homogène, vous pouvez convertir l'équation différentielle en une équation caractéristique, qui vous résoudre en utilisant l'algèbre. Vous faites cela en substituant votre conjecture v (t) = e^kt de plus tôt dans l'équation différentielle homogène:

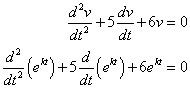
Factoring out e^kt vous mène à une équation caractéristique:

(k² + 5k +6)e^kt = 0

Le coefficient de e^kt doit être 0, de sorte que vous pouvez résoudre pour k comme suit:

k² + 5k + 6 = 0

k = -2. -3

Réglage de l'équation algébrique à 0 vous donne un équation caractéristique. Les racines constants -2 et -3 déterminent les caractéristiques de la solution v (t).

A partir de ces racines, vous obtenez une solution homogène qui est une combinaison des solutions e^-2t et e^-3t:

v (t) = c₁e^-2t + c₂e^-3t

Les constantes c₁ et c₂ sont déterminés par les conditions initiales lorsque t = 0.